2022年初中数学浙教版九年级下册第一章解直角三角形 章末检测——普通版
试卷更新日期:2022-01-24 类型:单元试卷
一、单选题
-
1. 在正方形网格中, ABC的位置如图所示,点A、B、C均在格点上,则cosB的值为( )
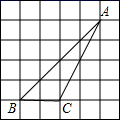 A、 B、 C、 D、2. 如图,四边形ABCD是菱形,AC=8,tan∠DAC= ,DH⊥AB于H,则点D到AB边距离等于( )
A、 B、 C、 D、2. 如图,四边形ABCD是菱形,AC=8,tan∠DAC= ,DH⊥AB于H,则点D到AB边距离等于( )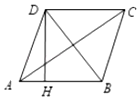 A、4 B、5 C、 D、3. 如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点 , 则AD的长是( )
A、4 B、5 C、 D、3. 如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点 , 则AD的长是( ) A、1 B、 C、 D、24. 如图,小慧的眼睛离地面的距离为 , 她用三角尺测量广场上的旗杆高度,仰角恰与三角板角的边重合,量得小慧与旗杆之间的距离为 , 则旗杆的高度(单位:m)为( )
A、1 B、 C、 D、24. 如图,小慧的眼睛离地面的距离为 , 她用三角尺测量广场上的旗杆高度,仰角恰与三角板角的边重合,量得小慧与旗杆之间的距离为 , 则旗杆的高度(单位:m)为( ) A、6.6 B、11.6 C、 D、5. 在Rt△ABC中,∠C=90°,sinA , 则cosB等于( )A、 B、 C、 D、6. 计算的值等于( )A、 B、1 C、3 D、7. 下表是小红填写的实践活动报告的部分内容:
A、6.6 B、11.6 C、 D、5. 在Rt△ABC中,∠C=90°,sinA , 则cosB等于( )A、 B、 C、 D、6. 计算的值等于( )A、 B、1 C、3 D、7. 下表是小红填写的实践活动报告的部分内容:
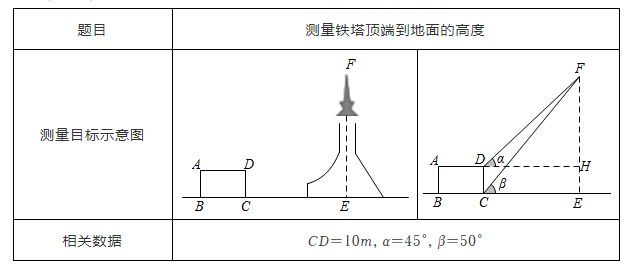
设铁塔顶端到地面的高度 为xm,根据以上条件,可以列出的方程为( )
A、 B、 C、 D、8. 点关于y轴对称的点的坐标是( )A、 B、 C、 D、9. 如图,PA、PB分别切⊙O于A,B,∠APB=60°,⊙O半径为2,则PB的长为( ) A、3 B、4 C、 D、10. 如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60海里的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A、3 B、4 C、 D、10. 如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60海里的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( ) A、30海里 B、60海里 C、120海里 D、(30+30)海里
A、30海里 B、60海里 C、120海里 D、(30+30)海里二、填空题
-
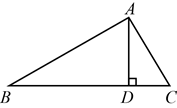
11. 如图,已知Rt ABC中,斜边BC上的高AD=4,cosB ,则AC=.
 12. 如图,矩形ABCD中,AB=4,AE=AD,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若F为CD中点,则BC的长为 .
12. 如图,矩形ABCD中,AB=4,AE=AD,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若F为CD中点,则BC的长为 . 13. 如图,AB为半圆O的直径,点C为半圆上的一点,CD⊥AB于点D,若AB=10,CD=4,则sin∠BCD的值为 .
13. 如图,AB为半圆O的直径,点C为半圆上的一点,CD⊥AB于点D,若AB=10,CD=4,则sin∠BCD的值为 . 14. 如图,将矩形 沿 折叠,点B恰好落在 的F处,若 ,则 值为= .
14. 如图,将矩形 沿 折叠,点B恰好落在 的F处,若 ,则 值为= . 15. 如图,A、B、C三点在正方形网格线的交点处,若将 绕着点A逆时针旋转得到 ,则tan ′的值为 .
15. 如图,A、B、C三点在正方形网格线的交点处,若将 绕着点A逆时针旋转得到 ,则tan ′的值为 . 16. 如图,在 和 中, , , , .则下列四个结论:① ;② ;③ ;④在 绕点 旋转过程中, 面积的最大值为 其中正确的是 . (填写所有正确结论的序号)
16. 如图,在 和 中, , , , .则下列四个结论:① ;② ;③ ;④在 绕点 旋转过程中, 面积的最大值为 其中正确的是 . (填写所有正确结论的序号)
三、解答题
-
17. 计算:(1)、 ;(2)、18. 某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得 , ,求出点D到AB的距离.(参考数据 , , )
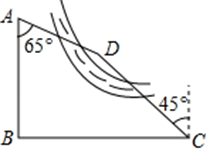 19. 如图,四边形 是平行四边形,联结 , .
19. 如图,四边形 是平行四边形,联结 , . (1)、求 的度数.(2)、求 的值.20. 如图,将一个直角三角形形状的楔子( )从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.如果楔子底面的斜角为 ,其高度 为 厘米,楔子沿水平方向前进一段距离(如箭头所示),留在外面的楔子长度 为 厘米.
(1)、求 的度数.(2)、求 的值.20. 如图,将一个直角三角形形状的楔子( )从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.如果楔子底面的斜角为 ,其高度 为 厘米,楔子沿水平方向前进一段距离(如箭头所示),留在外面的楔子长度 为 厘米.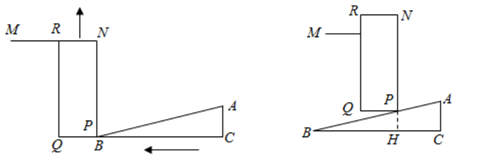 (1)、求 的长;(2)、木桩上升了多少厘米?( , , ,结果精确到 厘米)21. 某课桌生产厂家研究发现,倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度得桌面.新桌面的设计图如图1, 可绕点 旋转,在点 处安装一根长度一定且 处固定,可旋转的支撑臂 , .
(1)、求 的长;(2)、木桩上升了多少厘米?( , , ,结果精确到 厘米)21. 某课桌生产厂家研究发现,倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度得桌面.新桌面的设计图如图1, 可绕点 旋转,在点 处安装一根长度一定且 处固定,可旋转的支撑臂 , .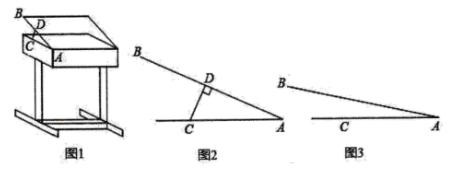
(参考数据: , , , )
(1)、如图2,当 时, ,求支撑臂 的长;(2)、如图3,当 时,求 的长.(结果保留根号)22. 图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.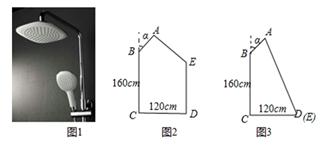 (1)、当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2)、如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
(1)、当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2)、如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据: ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
23. 如图,四边形 中, ,且满足 ,连结 . (1)、如图1,当 时,求证: .(2)、如图2,若 ,求 的值.(3)、如图3,延长 , 交于点D,连结 ,过点D作 ,若 , .试探究:在射线 上,是否存在点E,使得 的某一个内角等于 的2倍?若存在,连结 ,求 的值;若不存在,请说明理由.24. 测量金字塔高度
(1)、如图1,当 时,求证: .(2)、如图2,若 ,求 的值.(3)、如图3,延长 , 交于点D,连结 ,过点D作 ,若 , .试探究:在射线 上,是否存在点E,使得 的某一个内角等于 的2倍?若存在,连结 ,求 的值;若不存在,请说明理由.24. 测量金字塔高度如图1,金字塔是正四棱锥S-ABCD,点O是正方形ABCD的中心,SO垂直于地面,是正四棱锥S-ABCD的高.泰勒斯借助太阳光,测量金字塔影子△PBC的相关数据,利用平行投影测算出了金字塔的高度,受此启发,人们对甲、乙、丙三个金字塔高度也进行了测量,甲、乙、丙三个金字塔都用图1的正四棱锥S-ABCD表示.
 (1)、测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形ABCD的边长为80m,金字塔甲的影子是△PBC,PC=PB=50m,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.
(1)、测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形ABCD的边长为80m,金字塔甲的影子是△PBC,PC=PB=50m,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.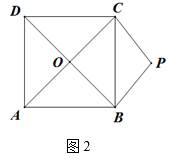 (2)、测量乙金字塔高度:如图1,乙金字塔底座正方形ABCD的边长为80m,金字塔乙的影子是△PBC,∠PCB=75°,PC= m,此刻,1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.(3)、测量丙金字塔高度:如图3,是丙金字塔的俯视图,测得底座正方形ABCD的边长为56m,金字塔丙的影子是△PBC,PC=60m,PB=52m,此刻,1米的标杆影长为0.8米,请利用已测出的数据,计算丙金字塔的高度.(精确到0.1)( )
(2)、测量乙金字塔高度:如图1,乙金字塔底座正方形ABCD的边长为80m,金字塔乙的影子是△PBC,∠PCB=75°,PC= m,此刻,1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.(3)、测量丙金字塔高度:如图3,是丙金字塔的俯视图,测得底座正方形ABCD的边长为56m,金字塔丙的影子是△PBC,PC=60m,PB=52m,此刻,1米的标杆影长为0.8米,请利用已测出的数据,计算丙金字塔的高度.(精确到0.1)( )