2022年初中数学浙教版九年级下册1.3解直角三角形 能力阶梯训练——普通版
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
1. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、2. 如图,中, ,点D在上, . 若 , 则的长度为( )
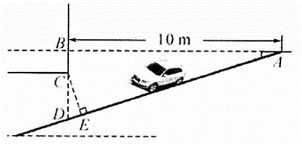
 A、 B、 C、 D、3. 如图,学校环保社成员想测得斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,且坡度为 , 则树AB的高度是 ( )
A、 B、 C、 D、3. 如图,学校环保社成员想测得斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,且坡度为 , 则树AB的高度是 ( )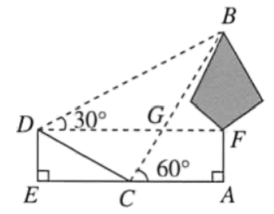 A、 B、30m C、 D、40m4. 如图,学校旁边一处斜坡OA上有一棵风景树,树高BC为6.5米,903班数学活动小组在某个时刻测得树的影长CD为2.5米,此时阳光恰好垂直照射在斜坡上,则这个斜坡的坡度为( )
A、 B、30m C、 D、40m4. 如图,学校旁边一处斜坡OA上有一棵风景树,树高BC为6.5米,903班数学活动小组在某个时刻测得树的影长CD为2.5米,此时阳光恰好垂直照射在斜坡上,则这个斜坡的坡度为( ) A、1:2.6 B、1:2.4 C、12:13 D、13:125. 下表是小红填写的实践活动报告的部分内容:
A、1:2.6 B、1:2.4 C、12:13 D、13:125. 下表是小红填写的实践活动报告的部分内容:
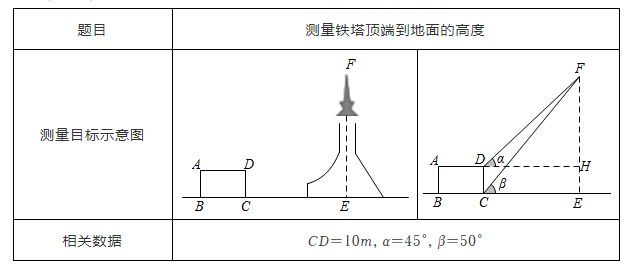
设铁塔顶端到地面的高度 为xm,根据以上条件,可以列出的方程为( )
A、 B、 C、 D、二、填空题
-
6. 如图,在中,已知 , , , 则 .
 7. 如图,在 中, , , 的垂直平分线 交 于 ,连接 .若 ,则 .
7. 如图,在 中, , , 的垂直平分线 交 于 ,连接 .若 ,则 . 8. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R= , 则C= , ≈(结果精确到0.01,参考数据:≈2.449,≈1.414).9. 如图,小明家附近有一观光塔CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他往前再走5米到达点B(点A,B,C在同一直线上),塔顶D的仰角为53°,则观光塔CD的高度约为 .(精确到0.1米,参考数值:tan37°≈ ,tan53°≈ )
8. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R= , 则C= , ≈(结果精确到0.01,参考数据:≈2.449,≈1.414).9. 如图,小明家附近有一观光塔CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他往前再走5米到达点B(点A,B,C在同一直线上),塔顶D的仰角为53°,则观光塔CD的高度约为 .(精确到0.1米,参考数值:tan37°≈ ,tan53°≈ )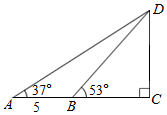 10. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .
10. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .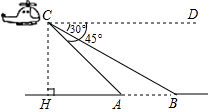
三、综合题
-
11. 汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,、分别为汽车两侧盲区的示意图,已知视线与地面的夹角 , 视线与地面的夹角 , 点A,F分别为 , 与车窗底部的交点, , , 垂直地面 , A点到B点的距离 . (参考数据: , , )
 (1)、求盲区中的长度;(2)、点M在上, , 在M处有一个高度为的物体,驾驶员能观察到物体吗?请说明.
(1)、求盲区中的长度;(2)、点M在上, , 在M处有一个高度为的物体,驾驶员能观察到物体吗?请说明.