2022年初中数学浙教版九年级下册1.2锐角三角函数的计算 能力阶梯训练——普通版
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
1. 下列各式中正确的是( )A、 B、 C、 D、2. 已知角α为ABC的内角,且cosα= , 则α的取值范围是( )A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°3. 如图,△ABC是锐角三角形,sinC= ,则sin A的取值范围是( )
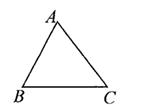 A、0<sinA< B、 <SinA<1 C、 <sinA< D、 <sinA<14. 如图,梯子(长度不变)跟地面所成的锐角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A、0<sinA< B、 <SinA<1 C、 <sinA< D、 <sinA<14. 如图,梯子(长度不变)跟地面所成的锐角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )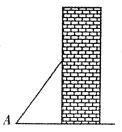 A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关5. 如图,小红同学测量一棵与地面垂直的树的高度时,在距离树的底端米的处,测得树顶的仰角 , 借助计算器计算树的高度,下列按键顺序正确的是( )
A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关5. 如图,小红同学测量一棵与地面垂直的树的高度时,在距离树的底端米的处,测得树顶的仰角 , 借助计算器计算树的高度,下列按键顺序正确的是( )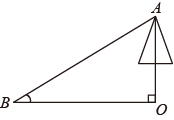 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 若三个锐角 满足 ,则 由小到大的顺序为.7. 已知 ,且 为锐角,则m的取值范围是 .8. 比较大小: (填“ ”“ ”或“>”)9. 如图所示的网格是正方形网格,则 (填“>”、“=”或“<”).
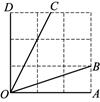 10. 下列结论中(其中 , 均为锐角),正确的是 . (填序号)
10. 下列结论中(其中 , 均为锐角),正确的是 . (填序号)① ;② ;③当 时, ;④ .
三、综合题
-
11. 如图,AB是⊙O的弦,半径OE⊥AB,P为AB的延长线上一点,PC与⊙O相切于点C,CE与AB交于点F.
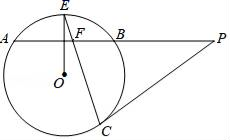 (1)、求证:PC=PF;(2)、连接OB,BC,若OB∥PC,BC=3 ,tanP= ,求FB的长.12.(1)、完成下列表格,并回答下列问题,
(1)、求证:PC=PF;(2)、连接OB,BC,若OB∥PC,BC=3 ,tanP= ,求FB的长.12.(1)、完成下列表格,并回答下列问题,锐角
(2)、当锐角 逐渐增大时, 的值逐渐 , 的值逐渐 , 的值逐渐 .(3)、 , ;(4)、 ;(5)、 ;(6)、若 ,则锐角 .13. 图1是一台实物投影仪,图2是它的示意图,折线 表示固定支架, 垂直水平桌面 于点 ,点 为旋转点, 可转动,当 绕点 顺时针旋转时,投影探头 始终垂直于水平桌面 ,经测量: , , , .(结果精确到0.1)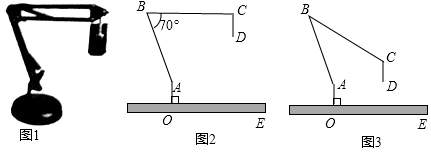 (1)、如图2, , .
(1)、如图2, , .①填空: °;
②求投影探头的端点 到桌面 的距离 .
(2)、如图3,将(1)中的 向下旋转,当投影探头的端点 到桌面 的距离为 时,求 的大小.(参考数据: , , , )14. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整)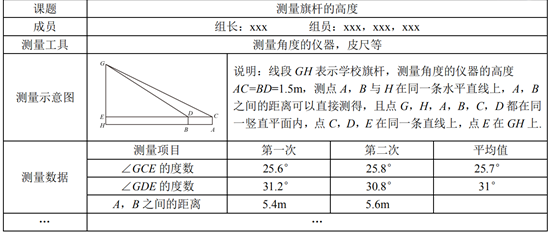
 (1)、任务一:两次测量A,B之间的距离的平均值是m.(2)、任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
(1)、任务一:两次测量A,B之间的距离的平均值是m.(2)、任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(3)、任务三:该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可).15. 如图所示,一种适用于笔记本电脑的铝合金支架,边 , 可绕点 开合,在 边上有一固定点 ,支柱 可绕点 转动,边 上有六个卡孔,其中离点 最近的卡孔为 ,离点 最远的卡孔为 .当支柱端点 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得 的长为 , 为 ,支柱 为 .
 (1)、当支柱的端点 放在卡孔 处时,求 的度数;(2)、当支柱的端点 放在卡孔 处时, ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
(1)、当支柱的端点 放在卡孔 处时,求 的度数;(2)、当支柱的端点 放在卡孔 处时, ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)