2021-2022学年浙教版数学九下1.3 解直角三角形同步练习
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
1. 如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点 , 则AD的长是( )
 A、1 B、 C、 D、22. 在Rt△ABC中,∠C=90°,sinA , 则cosB等于( )A、 B、 C、 D、3. 如图,小慧的眼睛离地面的距离为 , 她用三角尺测量广场上的旗杆高度,仰角恰与三角板角的边重合,量得小慧与旗杆之间的距离为 , 则旗杆的高度(单位:m)为( )
A、1 B、 C、 D、22. 在Rt△ABC中,∠C=90°,sinA , 则cosB等于( )A、 B、 C、 D、3. 如图,小慧的眼睛离地面的距离为 , 她用三角尺测量广场上的旗杆高度,仰角恰与三角板角的边重合,量得小慧与旗杆之间的距离为 , 则旗杆的高度(单位:m)为( ) A、6.6 B、11.6 C、 D、4. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( )
A、6.6 B、11.6 C、 D、4. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( ) A、米 B、米 C、米 D、米5. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
A、米 B、米 C、米 D、米5. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( ) A、2sin50° B、2sin40° C、2tan50° D、2tan40°6. 如图,学校环保社成员想测得斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,且坡度为 , 则树AB的高度是 ( )
A、2sin50° B、2sin40° C、2tan50° D、2tan40°6. 如图,学校环保社成员想测得斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,且坡度为 , 则树AB的高度是 ( )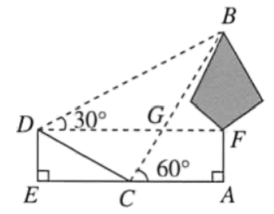 A、 B、30m C、 D、40m7. 如图,是的内接三角形, , 是直径, , 则的长为( )
A、 B、30m C、 D、40m7. 如图,是的内接三角形, , 是直径, , 则的长为( ) A、4 B、 C、 D、8. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、9. 如图,中, ,点D在上, . 若 , 则的长度为( )
A、4 B、 C、 D、8. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、9. 如图,中, ,点D在上, . 若 , 则的长度为( ) A、 B、 C、 D、10. 如图, 中, , , ,过点 作 于 ,过点 作 于 ,过点 作 于 ,这样继续作下去,线段 ( 为正整数)等于( ).
A、 B、 C、 D、10. 如图, 中, , , ,过点 作 于 ,过点 作 于 ,过点 作 于 ,这样继续作下去,线段 ( 为正整数)等于( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中,是边上的高, , , , 则的长为 .
 12. 如图,在中,已知 , , , 则 .
12. 如图,在中,已知 , , , 则 . 13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R= , 则C= , ≈(结果精确到0.01,参考数据:≈2.449,≈1.414).14. 如图,小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他每向前走60m,他的高度就升高36m,则这个斜坡的坡度等于.
13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R= , 则C= , ≈(结果精确到0.01,参考数据:≈2.449,≈1.414).14. 如图,小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他每向前走60m,他的高度就升高36m,则这个斜坡的坡度等于.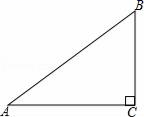 15. 如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了5米,那么物体离地面的高度为 .
15. 如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了5米,那么物体离地面的高度为 .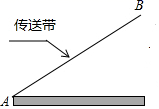 16. 如图,小明家附近有一观光塔CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他往前再走5米到达点B(点A,B,C在同一直线上),塔顶D的仰角为53°,则观光塔CD的高度约为 .(精确到0.1米,参考数值:tan37°≈ ,tan53°≈ )
16. 如图,小明家附近有一观光塔CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他往前再走5米到达点B(点A,B,C在同一直线上),塔顶D的仰角为53°,则观光塔CD的高度约为 .(精确到0.1米,参考数值:tan37°≈ ,tan53°≈ )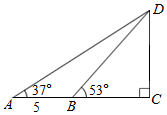
三、综合题
-
17. 如图①是某中型挖掘机,该挖掘机是由基座、主臂和伸展臂构成,图②是共侧面结构示意图(MN是基座,AB是主臂,BC是伸展臂),若主臂AB长为4米,主臂伸展角∠MAB的范围是:30°≤∠MAB≤60°,伸展臂伸展角∠ABC的范围是:45°≤∠ABC≤105°.
 (1)、如图③,当∠MAB=45°,伸展臂BC恰好垂直并接触地面时,求伸展臂BC的长(结果保留根号);(2)、若(1)中BC长度不变,求该挖掘机最远能挖掘到距A水平正前方多少米的土石.(结果保留根号)18. “太阳鸟”是我市文化广场的标志性雕塑.某“数学综合与实践”小组为了测量“太阳鸟”的高度,利用双休日通过实地测量(如示意图)和查阅资料,得到了以下信息:
(1)、如图③,当∠MAB=45°,伸展臂BC恰好垂直并接触地面时,求伸展臂BC的长(结果保留根号);(2)、若(1)中BC长度不变,求该挖掘机最远能挖掘到距A水平正前方多少米的土石.(结果保留根号)18. “太阳鸟”是我市文化广场的标志性雕塑.某“数学综合与实践”小组为了测量“太阳鸟”的高度,利用双休日通过实地测量(如示意图)和查阅资料,得到了以下信息:信息一:在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°.
信息二:在处用同一测角仪测得最高点A的仰角为45°.
信息三:测得米,点D、、B在同一条直线上.
信息四:参考数据: , , .

请根据以上信息,回答下列问题:
(1)、在中,(填sin32.6°、cos32.6°或tan32.6°),∴(填0.54、0.84或0.64).设米,则(用含x的代数式表示)米,(用含x的代数式表示)米.
(2)、在(1)的条件下,结合题中信息,求出x的值.(3)、“太阳鸟”的高度AB约为(精确到0.1)米.19. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.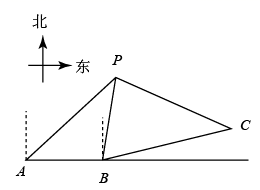 (1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)20. 汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,、分别为汽车两侧盲区的示意图,已知视线与地面的夹角 , 视线与地面的夹角 , 点A,F分别为 , 与车窗底部的交点, , , 垂直地面 , A点到B点的距离 . (参考数据: , , )
(1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)20. 汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,、分别为汽车两侧盲区的示意图,已知视线与地面的夹角 , 视线与地面的夹角 , 点A,F分别为 , 与车窗底部的交点, , , 垂直地面 , A点到B点的距离 . (参考数据: , , ) (1)、求盲区中的长度;(2)、点M在上, , 在M处有一个高度为的物体,驾驶员能观察到物体吗?请说明.21. 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)、求盲区中的长度;(2)、点M在上, , 在M处有一个高度为的物体,驾驶员能观察到物体吗?请说明.21. 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上. (1)、分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).(2)、已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险﹖请说明理由.(参考数据: , , 精确到1海里)22. 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
(1)、分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).(2)、已知距观测点D处100海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险﹖请说明理由.(参考数据: , , 精确到1海里)22. 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.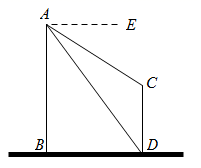 (1)、求两建筑物底部之间的水平距离BD;(2)、求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)23. 淮北市为缓解“停车难”问题.建造地下停车库,如图已知 , , C在BD上, . 根据规定,停车库坡道入口上方要张贴限高标准值,以告知驾驶员能否安全驶入.小明认为CD的长就是限高值,而小亮认为应该以CE的长作为限高值.(参考数据: , , , 结果精确到)
(1)、求两建筑物底部之间的水平距离BD;(2)、求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)23. 淮北市为缓解“停车难”问题.建造地下停车库,如图已知 , , C在BD上, . 根据规定,停车库坡道入口上方要张贴限高标准值,以告知驾驶员能否安全驶入.小明认为CD的长就是限高值,而小亮认为应该以CE的长作为限高值.(参考数据: , , , 结果精确到)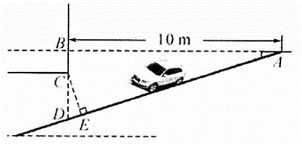 (1)、请你判断小明和小亮谁说的对?(2)、计算出正确的限高值.24. 如图,△ABC中,BD平分∠ABC,E为BC上一点,∠BDE=∠BAD=90°,
(1)、请你判断小明和小亮谁说的对?(2)、计算出正确的限高值.24. 如图,△ABC中,BD平分∠ABC,E为BC上一点,∠BDE=∠BAD=90°, (1)、求证:BD2=BA·BE;(2)、若AB=6,BE=8,求CD的长.25. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时50海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.
(1)、求证:BD2=BA·BE;(2)、若AB=6,BE=8,求CD的长.25. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时50海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.
(参考数据: ≈1.414, ≈1.732)
(1)、求∠APB的度数.(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?26. 图1是一台实物投影仪,图2是它的示意图,折线 表示固定支架, 垂直水平桌面 于点 ,点 为旋转点, 可转动,当 绕点 顺时针旋转时,投影探头 始终垂直于水平桌面 ,经测量: , , , .(结果精确到0.1) (1)、如图2, , .
(1)、如图2, , .①填空: ▲ °;
②求投影探头的端点 到桌面 的距离.
(2)、如图3,将(1)中的 向下旋转,当投影探头的端点 到桌面 的距离为 时,求 的大小.(参考数据: , , , )