2021-2022学年浙教版数学九下1.2 锐角三角函数的计算同步练习
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
1. 已知角α为ABC的内角,且cosα= , 则α的取值范围是( )A、0°<α<30° B、30°<α<45° C、45°<α<60° D、60°<α<90°2. 如图,已知:45°<A<90°,则下列各式成立的是( )
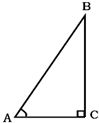 A、sinA=cosA B、sinA>cosA C、sinA>tanA D、sinA<cosA3. 若用我们数学课本上采用的科学计算器计算sin36 18',按键顺序正确的是( )A、
A、sinA=cosA B、sinA>cosA C、sinA>tanA D、sinA<cosA3. 若用我们数学课本上采用的科学计算器计算sin36 18',按键顺序正确的是( )A、 B、
B、 C、
C、 D、
D、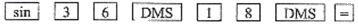 4. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )
4. 如图,在 中, , , ,若用科学计算器求AC的长,则下列按键顺序正确的是( )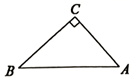 A、 B、 C、 D、5. 下列各式中正确的是( )A、 B、 C、 D、6. 如果锐角 的正切值为 ,那么下列结论中正确的是( )A、 B、 C、 D、7. 如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A、 B、 C、 D、5. 下列各式中正确的是( )A、 B、 C、 D、6. 如果锐角 的正切值为 ,那么下列结论中正确的是( )A、 B、 C、 D、7. 如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )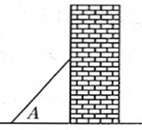 A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关8. 如图,为方便行人推车过天桥,某市政府在 高的天桥两端分别修建了 长的斜道,用科学计算器计算这条斜道的倾斜角 ,下列按键顺序正确的是( ).
A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关8. 如图,为方便行人推车过天桥,某市政府在 高的天桥两端分别修建了 长的斜道,用科学计算器计算这条斜道的倾斜角 ,下列按键顺序正确的是( ). A、
A、 B、
B、 C、
C、 D、
D、 9. 用计算器求 的值,以下按键顺序正确的是( )A、
9. 用计算器求 的值,以下按键顺序正确的是( )A、 B、
B、 C、
C、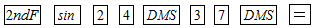 D、
D、 10. 已知 ,运用科学计算器求锐角 时(在开机状态下),按下的第一个键是( )A、
10. 已知 ,运用科学计算器求锐角 时(在开机状态下),按下的第一个键是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
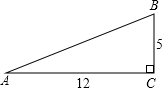
11. 如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,则AB= ,∠A= , ∠B= . (角度精确到1′)
 12. 下列结论中(其中 , 均为锐角),正确的是 . (填序号)
12. 下列结论中(其中 , 均为锐角),正确的是 . (填序号)① ;② ;③当 时, ;④ .
13. 如图,点P在正方形ABCD的BC边上,连接AP,作AP的垂直平分线,交AD延长线于点E,连接PE,交CD于点F.若点F是CD的中点,则tan∠BAP=. 14. 若三个锐角 满足 ,则 由小到大的顺序为.15. 比较大小: (填“ ”“ ”).16. 如图所示的网格是正方形网格,则 (填“>”、“=”或“<”).
14. 若三个锐角 满足 ,则 由小到大的顺序为.15. 比较大小: (填“ ”“ ”).16. 如图所示的网格是正方形网格,则 (填“>”、“=”或“<”).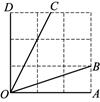 17. 已知 ,且 为锐角,则m的取值范围是 .18. 比较大小: (填“ ”“ ”或“>”)
17. 已知 ,且 为锐角,则m的取值范围是 .18. 比较大小: (填“ ”“ ”或“>”)三、综合题
-
19. 如图,AB是⊙O的弦,半径OE⊥AB,P为AB的延长线上一点,PC与⊙O相切于点C,CE与AB交于点F.
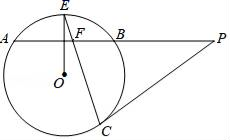 (1)、求证:PC=PF;(2)、连接OB,BC,若OB∥PC,BC=3 ,tanP= ,求FB的长.20. 今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体.
(1)、求证:PC=PF;(2)、连接OB,BC,若OB∥PC,BC=3 ,tanP= ,求FB的长.20. 今年疫情期间,针对各种入口处人工测量体温存在的感染风险高、效率低等问题,清华大学牵头研制一款“测温机器人”,如图1,机器人工作时,行人抬手在测温头处测量手腕温度,体温合格则机器人抬起臂杆行人可通行,不合格时机器人不抬臂杆并报警,从而有效阻隔病原体. (1)、为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:
(1)、为了设计“测温机器人”的高度,科研团队采集了大量数据.下表是抽样采集某一地区居民的身高数据:测量对象
男性(18~60岁)
女性(18~55岁)
抽样人数(人)
2000
5000
20000
2000
5000
20000
平均身高(厘米)
173
175
176
164
165
164
根据你所学的知识,若要更准确的表示这一地区男、女的平均身高,男性应采用厘米,女性应采用厘米;
(2)、如图2,一般的,人抬手的高度与身高之比为黄金比时给人的感觉最舒适,由此利用(1)中的数据得出测温头点P距地面105厘米.指示牌挂在两臂杆AB,AC的连接点A处,A点距地面110厘米.臂杆落下时两端点B,C在同一水平线上,BC=100厘米,点C在点P的正下方5厘米处.若两臂杆长度相等,求两臂杆的夹角.(参考数据表)
计算器按键顺序
计算结果(近似值)
计算器按键顺序
计算结果(近似值)
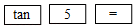
0.1

78.7
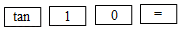
0.2

84.3

1.7
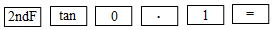
5.7

3.5
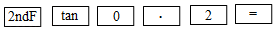
11.3
21.(1)、完成下列表格,并回答下列问题,锐角
(2)、当锐角 逐渐增大时, 的值逐渐 , 的值逐渐 , 的值逐渐 .(3)、 , ;(4)、 ;(5)、 ;(6)、若 ,则锐角 .22. 图1是一台实物投影仪,图2是它的示意图,折线 表示固定支架, 垂直水平桌面 于点 ,点 为旋转点, 可转动,当 绕点 顺时针旋转时,投影探头 始终垂直于水平桌面 ,经测量: , , , .(结果精确到0.1)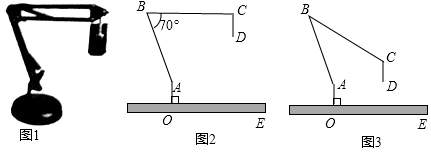 (1)、如图2, , .
(1)、如图2, , .①填空: °;
②求投影探头的端点 到桌面 的距离 .
(2)、如图3,将(1)中的 向下旋转,当投影探头的端点 到桌面 的距离为 时,求 的大小.(参考数据: , , , )23. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整)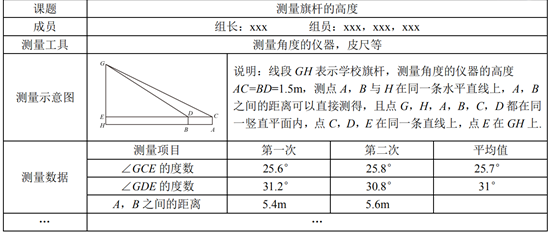
 (1)、任务一:两次测量A,B之间的距离的平均值是m.(2)、任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
(1)、任务一:两次测量A,B之间的距离的平均值是m.(2)、任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
(3)、任务三:该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可).24. 如图所示,一种适用于笔记本电脑的铝合金支架,边 , 可绕点 开合,在 边上有一固定点 ,支柱 可绕点 转动,边 上有六个卡孔,其中离点 最近的卡孔为 ,离点 最远的卡孔为 .当支柱端点 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得 的长为 , 为 ,支柱 为 .
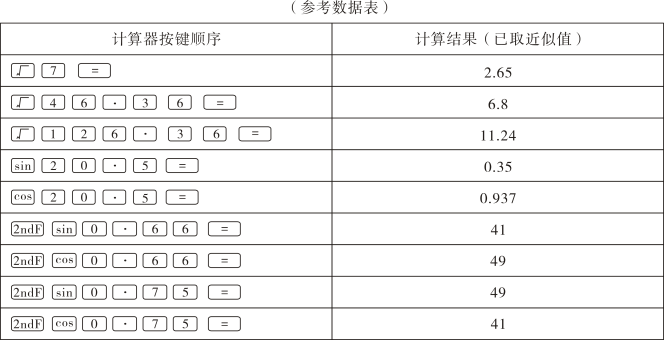 (1)、当支柱的端点 放在卡孔 处时,求 的度数;(2)、当支柱的端点 放在卡孔 处时, ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)25. 如图1,已知抛物线 过点 .
(1)、当支柱的端点 放在卡孔 处时,求 的度数;(2)、当支柱的端点 放在卡孔 处时, ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)25. 如图1,已知抛物线 过点 . (1)、求抛物线的解析式及其顶点C的坐标;(2)、设点D是x轴上一点,当 时,求点D的坐标;(3)、如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N, 和 的面积分别为 ,求 的最大值.26. 已知在梯形ABCD中,AD∥BC , AC=BC=10,cos∠ACB= ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB , DE的延长线与射线CB交于点F , 设AD的长为x .
(1)、求抛物线的解析式及其顶点C的坐标;(2)、设点D是x轴上一点,当 时,求点D的坐标;(3)、如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N, 和 的面积分别为 ,求 的最大值.26. 已知在梯形ABCD中,AD∥BC , AC=BC=10,cos∠ACB= ,点E在对角线AC上(不与点A、C重合),∠EDC=∠ACB , DE的延长线与射线CB交于点F , 设AD的长为x .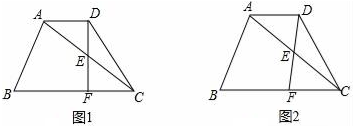 (1)、如图1,当DF⊥BC时,求AD的长;(2)、设EC=y , 求y关于x的函数解析式,并直接写出定义域;(3)、当△DFC是等腰三角形时,求AD的长.
(1)、如图1,当DF⊥BC时,求AD的长;(2)、设EC=y , 求y关于x的函数解析式,并直接写出定义域;(3)、当△DFC是等腰三角形时,求AD的长.