2021-2022学年初数北师大版九下第一章直角三角形的边角关系 单元检测
试卷更新日期:2022-01-24 类型:单元试卷
一、单选题
-
1. sin45°的值为( )A、 B、 C、1 D、2. 的值为( )A、1 B、 C、2 D、3. 若cosA ,则锐角∠A为( )A、30° B、15° C、45° D、60°4. 在Rt中, , 则的值为( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°, AC=3,BC=4,则sinA的值为( )
 A、 B、 C、 D、6. 如图,小慧的眼睛离地面的距离为 , 她用三角尺测量广场上的旗杆高度,仰角恰与三角板角的边重合,量得小慧与旗杆之间的距离为 , 则旗杆的高度(单位:m)为( )
A、 B、 C、 D、6. 如图,小慧的眼睛离地面的距离为 , 她用三角尺测量广场上的旗杆高度,仰角恰与三角板角的边重合,量得小慧与旗杆之间的距离为 , 则旗杆的高度(单位:m)为( ) A、6.6 B、11.6 C、 D、7. 如图,在的正方形网格中,每个小正方形的边长均为1,已知的顶点位于正方形网格的格点上,且 , 则满足条件的是( )A、
A、6.6 B、11.6 C、 D、7. 如图,在的正方形网格中,每个小正方形的边长均为1,已知的顶点位于正方形网格的格点上,且 , 则满足条件的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED=( )
8. 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED=( ) A、 B、 C、 D、9. 在中,∠ , , 则的值为( )A、 B、 C、 D、10. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、11. 如图,中, ,点D在上, . 若 , 则的长度为( )
A、 B、 C、 D、9. 在中,∠ , , 则的值为( )A、 B、 C、 D、10. 一架5米长的梯子斜靠在墙上,测得它与地面的夹角为 , 则梯子底端到墙角的距离为( )A、 B、 C、 D、11. 如图,中, ,点D在上, . 若 , 则的长度为( ) A、 B、 C、 D、12. 在边长为1的正方形组成的网格中,线段AB,CD的端点都在格点上,AB,CD交于点E,则tan∠AED的值为( )
A、 B、 C、 D、12. 在边长为1的正方形组成的网格中,线段AB,CD的端点都在格点上,AB,CD交于点E,则tan∠AED的值为( ) A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
13. 已知α是锐角,如果 ,那么α= .14. 若tan(a+10°)= ,则锐角a= .15. 已知 为锐角,且 ,则 度数等于度.16. 若sin(x﹣30°)= ,则x=.17. 在中, , , 则 .18. 如图,在5×4的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为 .

三、计算题
-
19. 计算(1)、(2)、已知 是锐角,且 ,计算 的值.20. 如图,在Rt△ABC中, ,D是AB的中点,过D点作AB的垂线交AC于点E,若BC=6,sinA= ,求DE的长.
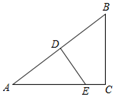
21. 等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.) 22. 如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度( ,结果保留一位小数).
22. 如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度( ,结果保留一位小数).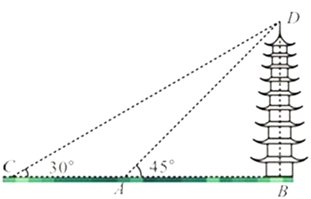 23. 如图,从楼层底部 处测得旗杆 的顶端 处的仰角是 ,从楼层顶部 处测得旗杆 的顶端 处的仰角是 ,已知楼层 的楼高为 米.求旗杆 的高度约为多少米?(参考数据: )
23. 如图,从楼层底部 处测得旗杆 的顶端 处的仰角是 ,从楼层顶部 处测得旗杆 的顶端 处的仰角是 ,已知楼层 的楼高为 米.求旗杆 的高度约为多少米?(参考数据: )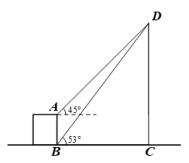 24. 如图,一艘轮船位于灯塔B的正西方向上的A处,且灯塔B到A处的距离为40海里,轮船沿东北方向匀速航行,速度为20海里/时.
24. 如图,一艘轮船位于灯塔B的正西方向上的A处,且灯塔B到A处的距离为40海里,轮船沿东北方向匀速航行,速度为20海里/时. (1)、多长时间后,轮船行驶到达位于灯塔B的西北方向上的C处?(结果保留根号)(2)、若轮船不改变方向行驶,当轮船行驶到达位于灯塔B的北偏东15°方向上的D处时,求灯塔B到D处的距离.(结果保留根号)25. 某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
(1)、多长时间后,轮船行驶到达位于灯塔B的西北方向上的C处?(结果保留根号)(2)、若轮船不改变方向行驶,当轮船行驶到达位于灯塔B的北偏东15°方向上的D处时,求灯塔B到D处的距离.(结果保留根号)25. 某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
求:
(1)、观众区的水平宽度AB;(2)、顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)26. “太阳鸟”是我市文化广场的标志性雕塑.某“数学综合与实践”小组为了测量“太阳鸟”的高度,利用双休日通过实地测量(如示意图)和查阅资料,得到了以下信息:信息一:在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°.
信息二:在处用同一测角仪测得最高点A的仰角为45°.
信息三:测得米,点D、、B在同一条直线上.
信息四:参考数据: , , .

请根据以上信息,回答下列问题:
(1)、在中,(填sin32.6°、cos32.6°或tan32.6°),∴(填0.54、0.84或0.64).设米,则(用含x的代数式表示)米,(用含x的代数式表示)米.
(2)、在(1)的条件下,结合题中信息,求出x的值.(3)、“太阳鸟”的高度AB约为(精确到0.1)米.