2021-2022学年浙教版数学九下1.1 锐角三角函数同步练习
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
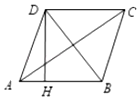
1. 如图,四边形ABCD是菱形,AC=8,tan∠DAC= ,DH⊥AB于H,则点D到AB边距离等于( )
 A、4 B、5 C、 D、2. 在Rt中, , 则的值为( )A、 B、 C、 D、3. 如图,在Rt△ABC中,∠C=90°, AC=3,BC=4,则sinA的值为( )
A、4 B、5 C、 D、2. 在Rt中, , 则的值为( )A、 B、 C、 D、3. 如图,在Rt△ABC中,∠C=90°, AC=3,BC=4,则sinA的值为( ) A、 B、 C、 D、4. 如图,在的正方形网格中,每个小正方形的边长均为1,已知的顶点位于正方形网格的格点上,且 , 则满足条件的是( )A、
A、 B、 C、 D、4. 如图,在的正方形网格中,每个小正方形的边长均为1,已知的顶点位于正方形网格的格点上,且 , 则满足条件的是( )A、 B、
B、 C、
C、 D、
D、 5. 计算的值等于( )A、 B、1 C、3 D、6. 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED=( )
5. 计算的值等于( )A、 B、1 C、3 D、6. 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则sin∠CED=( ) A、 B、 C、 D、7. 在中,∠ , , 则的值为( )A、 B、 C、 D、8. 点关于y轴对称的点的坐标是( )A、 B、 C、 D、9. 在4×4网格中,∠α的位置如图所示,则sinα的值为( )
A、 B、 C、 D、7. 在中,∠ , , 则的值为( )A、 B、 C、 D、8. 点关于y轴对称的点的坐标是( )A、 B、 C、 D、9. 在4×4网格中,∠α的位置如图所示,则sinα的值为( ) A、 B、 C、2 D、10. 在Rt△ABC中,∠C=90°,若∠A=30°,则sinA的值是( )A、 B、 C、 D、111. 如图,已知 是 的外接圆, 是 的直径,连结 .若 , ,则 的值为( )
A、 B、 C、2 D、10. 在Rt△ABC中,∠C=90°,若∠A=30°,则sinA的值是( )A、 B、 C、 D、111. 如图,已知 是 的外接圆, 是 的直径,连结 .若 , ,则 的值为( )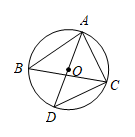 A、 B、 C、 D、12. Rt△ABC中,∠C=90°,若AB=4,cosA= , 则AC的长为( )A、 B、 C、 D、5
A、 B、 C、 D、12. Rt△ABC中,∠C=90°,若AB=4,cosA= , 则AC的长为( )A、 B、 C、 D、5二、填空题
-
13. 计算: × ﹣sin45°=.14. 如图,AB为半圆O的直径,点C为半圆上的一点,CD⊥AB于点D,若AB=10,CD=4,则sin∠BCD的值为 .
 15. 如图,A、B、C三点在正方形网格线的交点处,若将 绕着点A逆时针旋转得到 ,则tan ′的值为 .
15. 如图,A、B、C三点在正方形网格线的交点处,若将 绕着点A逆时针旋转得到 ,则tan ′的值为 . 16. 在中, , , 则 .17. 如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是
16. 在中, , , 则 .17. 如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是 18. 如图,在5×4的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为 .
18. 如图,在5×4的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为 . 19. 如图,P(12,a)在反比例函数图象上,PH⊥x轴于H,则tan∠POH的值为.
19. 如图,P(12,a)在反比例函数图象上,PH⊥x轴于H,则tan∠POH的值为.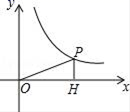
三、综合题
-
20. 如图,在平面直角坐标系中,A、B两点的坐标分别为(3,﹣1)、(2,1).
 (1)、以点O为位似中心,在点O的异侧将△OAB放大为原来的2倍,得到△OA1B1 , 请画出△OA1B1 .(2)、按照(1)的变换后,cos∠OA1B1= .(3)、设点P(a,b)为△OAB内部一点,按照(1)的变换后,点P在△OA1B1内部的对应点P1的坐标为 .21. 已知在△ABC中,∠C=90°,AB=4,AC= .
(1)、以点O为位似中心,在点O的异侧将△OAB放大为原来的2倍,得到△OA1B1 , 请画出△OA1B1 .(2)、按照(1)的变换后,cos∠OA1B1= .(3)、设点P(a,b)为△OAB内部一点,按照(1)的变换后,点P在△OA1B1内部的对应点P1的坐标为 .21. 已知在△ABC中,∠C=90°,AB=4,AC= .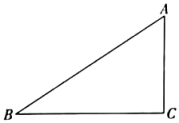 (1)、求BC;(2)、求sinA.22. 如图,在平行四边形ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
(1)、求BC;(2)、求sinA.22. 如图,在平行四边形ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.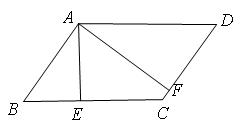 (1)、求证:∠BAE=∠DAF;(2)、已知AE=4,AF=6,tan∠BAE= , 求CF的长.23. 如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=
(1)、求证:∠BAE=∠DAF;(2)、已知AE=4,AF=6,tan∠BAE= , 求CF的长.23. 如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=
求:
(1)、反比例函数的解析式;(2)、点C的坐标;(3)、sin∠ABC的值.24. 如图,在平面直角坐标系中,已知点B的坐标为(﹣2,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点. (1)、求A,C两点的坐标;(2)、求抛物线的解析式;(3)、若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.25. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆⊙O交于点D,连结BD交AC于点F.
(1)、求A,C两点的坐标;(2)、求抛物线的解析式;(3)、若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.25. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆⊙O交于点D,连结BD交AC于点F. (1)、求证:BD=CD.(2)、若∠BAC=60°,BC=3,当AF将△ABD的面积分为1:2两部分时,求△ADF与△BCF的面积比值.(3)、将C点关于AD的对称点记为点C',当BC'= BD时,写出AD与半径r的数量关系,并说明理由.26. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.
(1)、求证:BD=CD.(2)、若∠BAC=60°,BC=3,当AF将△ABD的面积分为1:2两部分时,求△ADF与△BCF的面积比值.(3)、将C点关于AD的对称点记为点C',当BC'= BD时,写出AD与半径r的数量关系,并说明理由.26. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G. (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.
27. 如图,在△ABC中,AC=BC=2 ,tan∠CAB= ,P为AC上一点,PD⊥AB交AB于点E,AD⊥AC交PD于点D,连结BD,CD,CD交AB于点Q.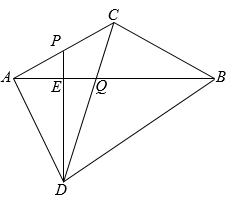 (1)、若CD⊥BC,求证:△AED∽△QCB;(2)、若AB平分∠CBD,求BQ的长;(3)、连结PQ并延长交BD于点M.当PM平行于四边形ADBC中的某一边时,直接写出 的值.
(1)、若CD⊥BC,求证:△AED∽△QCB;(2)、若AB平分∠CBD,求BQ的长;(3)、连结PQ并延长交BD于点M.当PM平行于四边形ADBC中的某一边时,直接写出 的值.