2021-2022学年初数北师大版九下1.6利用三角函数测高 同步测试
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
1. 如图,要得到从点D观测点A的俯角,可以测量( )
 A、∠ADC B、∠DCE C、∠ADB D、∠DAB2. 小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在 处测得顶端 的仰角∠ = , 到旗杆的距离 =5米,测角仪 的高度为1米,则旗杆 的高度表示为( ).
A、∠ADC B、∠DCE C、∠ADB D、∠DAB2. 小致利用测角仪和皮尺测量学校旗杆的高度,如图,小致在 处测得顶端 的仰角∠ = , 到旗杆的距离 =5米,测角仪 的高度为1米,则旗杆 的高度表示为( ).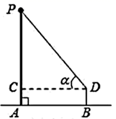 A、5 +1 B、5 +1 C、5 +1 D、 +13. 河堤横断面如图所示,堤高 米,迎水坡 的坡比为 ,则AB的长为( )
A、5 +1 B、5 +1 C、5 +1 D、 +13. 河堤横断面如图所示,堤高 米,迎水坡 的坡比为 ,则AB的长为( )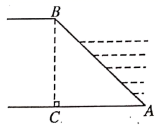 A、 米 B、 米 C、18米 D、21米4. 如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=12米,则树的高AB(单位:米)为( )
A、 米 B、 米 C、18米 D、21米4. 如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=12米,则树的高AB(单位:米)为( )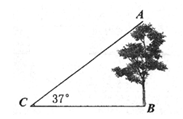 A、 B、 C、12tan37° D、12sin37°5. 如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )
A、 B、 C、12tan37° D、12sin37°5. 如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )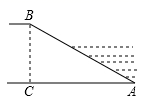 A、5m B、10m C、 m D、8m6. 如图是某一滑板场地的截面示意图, 于点B, , , .设斜坡 的坡度为i,则下列等式正确的是( )
A、5m B、10m C、 m D、8m6. 如图是某一滑板场地的截面示意图, 于点B, , , .设斜坡 的坡度为i,则下列等式正确的是( )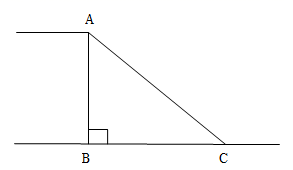 A、 B、 C、 D、7. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A、 B、 C、 D、7. 如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )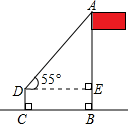 A、tan55°= B、tan55°= C、sin55°= D、cos55°=8. 如图,为测量一根与地面垂直的旗杆 的高度,在距离旗杆底端 10米的 处测得旗杆顶端 的仰角 ,则旗杆 的高度为( )
A、tan55°= B、tan55°= C、sin55°= D、cos55°=8. 如图,为测量一根与地面垂直的旗杆 的高度,在距离旗杆底端 10米的 处测得旗杆顶端 的仰角 ,则旗杆 的高度为( )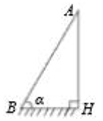 A、 米 B、 米 C、 米 D、 米9. 如图,从点 看一山坡上的电线杆 ,观测点 的仰角是 ,向前走 到达 点,测得顶端点 和杆底端点 的仰角分别是 和 ,则该电线杆 的高度为( )m.
A、 米 B、 米 C、 米 D、 米9. 如图,从点 看一山坡上的电线杆 ,观测点 的仰角是 ,向前走 到达 点,测得顶端点 和杆底端点 的仰角分别是 和 ,则该电线杆 的高度为( )m.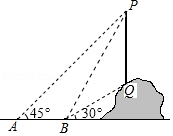 A、 B、 C、 D、10. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长 米,背水坡CD的坡度 ,则背水坡的坡长CD为( )米.
A、 B、 C、 D、10. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长 米,背水坡CD的坡度 ,则背水坡的坡长CD为( )米.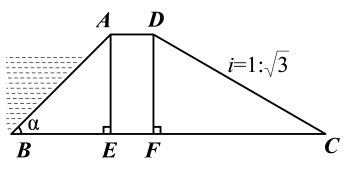 A、20 B、 C、10 D、
A、20 B、 C、10 D、二、填空题
-
11. 如图,有一个小山坡 ,坡比 .已知小山坡的水平距离 ,则小山坡的高度 是.
 12. 如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了5米,那么物体离地面的高度为 .
12. 如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了5米,那么物体离地面的高度为 .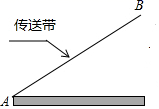 13. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .
13. 如图,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为 和 若飞机离地面的高度CH为1200米,且点H,A,B在同一水平直线上,则这条江的宽度AB为米 结果保留根号 .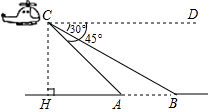 14. 如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m, ).
14. 如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度约为 m(结果精确到1m, ).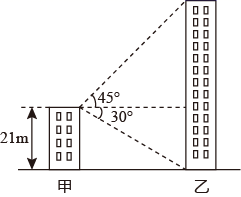 15. 如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为270米,则这栋大楼的高度为米.
15. 如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为270米,则这栋大楼的高度为米.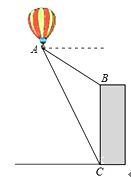
三、解答题
-
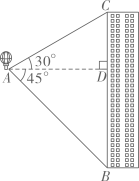
16. 热气球的探测器显示,从热气球A处看大楼BC顶部C的仰角为30°,看大楼底部B的俯角为45°,热气球与该楼的水平距离AD为60米,求大楼BC的高度.(结果精确到1米,参考数据: )
 17. 周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
17. 周末,小强在文化广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为58°,已知风筝线BC的长为10米,小强的身高AB为1.55米.请你帮小强画出测量示意图,并计算出风筝离地面的高度(结果精确到0.1米).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60) ]18. 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
]18. 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.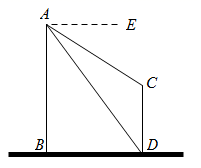 (1)、求两建筑物底部之间的水平距离BD;(2)、求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)
(1)、求两建筑物底部之间的水平距离BD;(2)、求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)