浙江省丽水市2021-2022学年七年级上学期数学期末考试试卷

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1. |-4|的相反数是（）

A、4 B、 $\frac{1}{4}$ C、-4 D、 $- \frac{1}{4}$

查看试题解析
2. 下列计算正确的是（）

A、（-1）+（-6）=+7 B、（-3）-（-4）=-7 C、（-4）×（-3）=12 D、（-3） ÷2=-1

查看试题解析
3. 实数在数轴上的位置如图所示，则下列各式正确的是（）

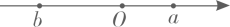A、a+b>0 B、a-b<0 C、ab>0 D、|b|>a

查看试题解析
4. 单项式 $- \frac{a b^{2}}{2}$ 的系数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
5. 如图∠AOC+∠COD-∠AOB=（）

A、∠AOC B、∠BOC C、∠BOD D、∠AOD

查看试题解析
6. 下列各式正确的是（）

A、a²+a²=a⁴ B、7ab-4ab=3 C、3a+5b=8ab D、-4a²b+3ba²=-a²b

查看试题解析
7. 近似数3.70所表示的准确值x的取值范围是（）

A、3.695≤x<3.705 B、3.60<x<3.80 C、3.695<x≤3.705 D、3.700<x≤3.705

查看试题解析
8. 如图，点C为线段AB的中点，点D为线段AC的中点，DB=9，则AB长为（）

A、 $\frac{27}{4}$ B、11 C、12 D、13.5

查看试题解析
9. 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是，有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为（）

A、24里 B、12里 C、6里 D、3里

查看试题解析
10. 有理数满足a+b<0，|a+b|=|a|-|b|，则下列结论正确的是（）

A、a<b<0 B、a>b>0 C、a<0<b D、b<a<0

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 若m²=（-3）² ，则m=

查看试题解析
12. 若a的3倍与a的相反数的和为8，则a=

查看试题解析
13. 如图是加工零件的尺寸要求，那么合格零件的直径尺寸的范围是。（单位：mm）

查看试题解析
14. 实数 $\sqrt{7}$ 的整数部分为a，小数部分为b，则 $\sqrt{7}$ （a²+ab）= ．

查看试题解析
15. 当x=1时，px³+qx+1=2021，则当x=-1时，px³+qx+1= ．

查看试题解析
16. 如图，A，C两点在直线l上，AC=6，点D为射线CM上一点，CD=7，若在A，C两点之间拴一根橡皮筋，“奋力牛”Q拉动橡皮筋在直线AC和射线CM所确定的平面内爬行，爬行过程中始终保持QA=nQC．

(1)、若n=3，点Q在直线l上，直接写出QC的长度：.

(2)、在“奋力牛”爬行过程中，nQD+QA的最小值是．

查看试题解析

三、解答题（本题有8小题，第17~22题每题6分，第23、24题每题8分，共52分，各小题都必须写出解答过程）

17. 计算

(1)、 $- 2^{4} \div \frac{4}{9} \times {(- \frac{3}{2})}^{2}$

(2)、 $- \frac{1}{60} \div (\frac{1}{3} + \frac{1}{4} - \frac{1}{5})$

查看试题解析
18. 解下列方程

(1)、x+8=3x+2

(2)、 $\frac{2 x - 1}{2} = \frac{x + 2}{4} - 1$

查看试题解析
19. 如图，已知线段AB和点P．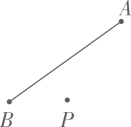

(1)、作射线BP；

(2)、用圆规在射线BP上作点C，连结AC，使AC=AB；（保留痕迹）

(3)、过点A画射线BP的垂线段AD，D为垂足；

(4)、比较大小：BDCD，∠BAD∠CAD．

查看试题解析
20. 已知P=ab-5a+3，Q=a-3ab+2．

(1)、当a=-1，b= $\frac{1}{3}$ 时，求3P-2Q的值．

(2)、当a≠0时，3P-2Q=5恒成立，求b的值．

查看试题解析
21. [x]表示不大于x的最大整数，如[3.25]=3，[5]=5，[-2.7]=-3，计算下列各题．

(1)、 $[\sqrt{1 \times 2}] + [\sqrt{2 \times 3}] + [\sqrt{3 \times 4}] + ... + [\sqrt{49 \times 50}]$

(2)、 $[^{3} \sqrt{1 \times 2 \times 3}] + [^{3} \sqrt{2 \times 3 \times 4}] + [^{3} \sqrt{3 \times 4 \times 5}] + ... + [^{3} \sqrt{48 \times 49 \times 50}]$

查看试题解析
22. 某校召开秋季运动会，七（1）、七（2）两班学生到超市买矿泉水，超市的销售方法如下：
每次购买不超过30瓶，按零售价销售，每瓶3元：每次购买超过30瓶但不超过50瓶，按零体价的八折销售：每次购买超过50瓶，按零售价六折销售．七（1）班分两天两次购买矿泉水70瓶（第二天多于第一天），共付183元，而七（2）班则一次性购买70瓶．

(1)、七（1）、七（2）两班哪个花钱多，多花多少？

(2)、七（1）班第一，第二天分别购买多少瓶？

查看试题解析
23. 已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC．

(1)、如图1，若∠AOC=30°，求∠DOE的度数．

(2)、在图1中，若∠AOC=α，求∠DOE的度数．（用含α的代数式表示）

(3)、将图1中的∠DOC绕顶点O顺时针旋转至图2的位置，且保持射线OC在直线AB上方，在整个旋转过程中，当∠AOC的度数是多少时，∠COE=2∠DOB．

查看试题解析

24. 一组连续奇数按如图方式排列，请你解决下列问题：

	第1列	第2列	第3列	第4列	第5列	第6列	……
第1行	1
第2行	3	5
第3行	7	9	11
第4行	13	15	17	19
第5行	21	23	25	27	29
第6行	31	33	35	37	39	41
……	……	……	……	……	……	……	……

(1)、第20行最后一个数字是，在第21行第4列的数字是．

(2)、奇数949位于第几行第几列？

(3)、现用一个正方形框去围出相邻两行中的4个数字（例如：第4行的15，17和第5行的23，25），请问能否在第50行和第51行中围出4个数字的和是10016？若能，请求出这4个数字；若不能，请说明理由．

查看试题解析