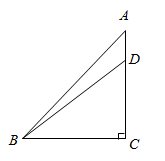2021-2022学年初数北师大版九下1.4解直角三角形 同步测试
试卷更新日期:2022-01-24 类型:同步测试
一、单选题
-
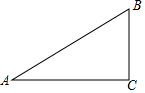
1. 在 中, ,则 的正弦值为( )A、 B、 C、2 D、2. 如图,在△ABC中,∠C=90°,cosA= ,则sinB=( )
 A、 B、 C、 D、3. 如图,在 中, , , ,则 长为( )
A、 B、 C、 D、3. 如图,在 中, , , ,则 长为( )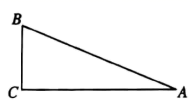 A、 B、 C、 D、4. 如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米.
A、 B、 C、 D、4. 如图,A、B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠A=90°,∠C=40°,则AB等于( )米. A、asin40° B、acos40° C、atan40° D、5. 关于直角三角形,下列说法正确的是( )A、所有的直角三角形一定相似 B、如果直角三角形的两边长分别是3和4,那么第三边的长一定是5 C、如果已知直角三角形两个元素(直角除外),那么这个直角三角形一定可解 D、如果已知直角三角形一锐角的三角函数值,那么这个直角三角形的三边之比一定确定6. 在 中, , , ,则 的值是( )A、 B、 C、 D、7. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( )
A、asin40° B、acos40° C、atan40° D、5. 关于直角三角形,下列说法正确的是( )A、所有的直角三角形一定相似 B、如果直角三角形的两边长分别是3和4,那么第三边的长一定是5 C、如果已知直角三角形两个元素(直角除外),那么这个直角三角形一定可解 D、如果已知直角三角形一锐角的三角函数值,那么这个直角三角形的三边之比一定确定6. 在 中, , , ,则 的值是( )A、 B、 C、 D、7. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( ) A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB8. 在Rt△ABC中,∠C=90°,sinA , 则cosB等于( )A、 B、 C、 D、9. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( )
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB8. 在Rt△ABC中,∠C=90°,sinA , 则cosB等于( )A、 B、 C、 D、9. 已知Rt△ABC中,∠C=90°,∠A=50°,AB=2,则AC=( ) A、2sin50° B、2sin40° C、2tan50° D、2tan40°10. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( )
A、2sin50° B、2sin40° C、2tan50° D、2tan40°10. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为5米.若栏杆的旋转角 , 则栏杆A端升高的高度为( ) A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米二、填空题
-
11. 已知在直角三角形ABC中,∠C为直角,tan∠ABC=2,AC=2,则AB= .12. 如图,在边长为1的小正方形网格中,点A、B、C均在格点上,则tan∠B的值为 .
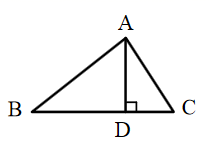
 13. 已知在Rt△ABC中,∠C=90°,sin A= ,则tan B的值为.14. 如图,在中,是边上的高, , , , 则的长为 .
13. 已知在Rt△ABC中,∠C=90°,sin A= ,则tan B的值为.14. 如图,在中,是边上的高, , , , 则的长为 . 15. 如图,在 中, , , ,点D是边 上的动点,过点D作 于E点.请探究下列问题:
15. 如图,在 中, , , ,点D是边 上的动点,过点D作 于E点.请探究下列问题: (1)、若 ,则 ;(2)、若 ,设点F是边 上的动点,连接 、 ,以 、 为邻边作平行四边形 ,且使得顶点G恰好落在 边上,则 .
(1)、若 ,则 ;(2)、若 ,设点F是边 上的动点,连接 、 ,以 、 为邻边作平行四边形 ,且使得顶点G恰好落在 边上,则 .三、解答题