2022年初中数学浙教版七年级下册2.5三元一次方程组及其解法 能力阶梯训练——普通版
试卷更新日期：2022-01-24 类型：同步测试
一、单选题
-
1. 方程组 的解是（ ）A、 B、 C、 D、2. 有铅笔、练习本、圆珠笔三种学习用品．若购铅笔3支，练习本7本，圆珠笔1支共需31元；若购铅笔4支，练习本10本，圆珠笔1支共需42元．现购铅笔，练习本，圆珠笔各1个，共需（ ）A、12元 B、10.5元 C、9.5元 D、9元3. 甲、乙、丙三种商品，若购买甲2件、乙4件、丙3件，共需220元钱，购甲3件、乙1件、丙2件共需235元钱，那么购甲、乙、丙三种商品各一件共需（ ）A、85元 B、89元 C、90元 D、91元4. 若 ， ，则x＋y＋z的值等于（ ）A、0 B、2 C、1 D、无法求出5. 某宾馆有单人间，双人间，三人间三种客房供游客选择居住，现某旅游团有20名旅客同时安排游客居住在该宾馆，若每个房间都住满，共租了9间客房，则居住方案（ ）A、1种 B、2种 C、3种 D、4种
二、填空题
-
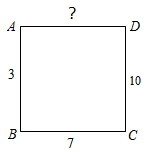
6. 如图，在正方形 的每个顶点上写一个数，然后把它的每条边的两个端点上的数加起来，将结果写在这条边上，若 边上的数字是3， 边上的数字是7， 边上的数字是10，则 边上的数字是.
7. 解方程组 时，消去字母z ， 得到含有未知数x ， y的二元一次方程组是 ．8. 盲盒为消费市场注入了活力，既能够营造消费者购物过程中的趣味体验，也为商家实现销售额提升拓展了途径.某商家将蓝牙耳机、多接口优盘、迷你音箱共22个，搭配为A，B，C三种盲盒各一个，其中A盒中有2个蓝牙耳机，3个多接口优盘，1个迷你音箱；B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量，蓝牙耳机与迷你音箱的数量之比为3：2；C盒中有1个蓝牙耳机，3个多接口优盘，2个迷你音箱.经核算，A盒的成本为145元，B盒的成本为245元（每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和），则C盒的成本为元.9. 农历五月初五，中国传统节日端午节.某超市为了吸引顾客，在端午节当天推出由白粽、豆沙粽、蛋黄粽三种不同的粽子搭配而成的A、B两种礼盒，其中，A种礼盒含4个白粽、3个豆沙粽、3个蛋黄粽；B种礼盒含2个白粽、4个豆沙粽、4个蛋黄粽.每种礼盒的成本价分别为三种粽子的成本价之和（包装成本忽略不计），已知每盒A种礼盒的总成本为1个白粽成本的13倍，每盒A种礼盒的利润率为20%，每盒B种礼盒的利润率为25%，则当销售A、B两种礼盒的数量之比为7：26时，则该超市销售这两种礼盒的总利润率为.10. “端午节”是我国的传统佳节，民间历来有吃粽子的习俗.某超市准备了515个豆沙粽，525个火腿粽和若干个腊肉棕，将这些粽子分成了A，B，C三类礼品盒进行包装.A类礼品盒里有4个豆沙粽，4个火腿粽和6个腊肉粽；B类礼品盒里有3个豆沙粽，5个火腿粽和6个腊肉粽；C类礼品盒里有6个豆沙粽，4个火腿粽和4个腊肉粽.已知A，B，C三类礼品盒的数量都为正整数，并且A类礼品盒少于44盒，B类礼品盒少于49盒.如果所有礼品盒里的腊肉粽的总个数为m，则m=三、计算题
-
11. 解方程组：12. 对于一个三位数 ，如果 满足：它的百位数字、十位数字之和与个位数字的差等于8，那么称这个数 为“快乐数”.例如： ， ， 是“快乐数”； ， ， 不是“快乐数”.(1)、判断844，735是否为“快乐数”？并说明理由；(2)、若将一个“快乐数” 的个位数的3倍放到百位，原来的百位数变成十位数，原来的十位数变成个位数，得到一个新的三位数 （例如：若 ，则 ），若 也是一个“快乐数”，求满足条件的所有 的值.13. （阅读感悟）
对于方程组的问题，有时候要求的结果不是每个未知数的值，而是求关于未知数的代数式的值.如已知实数 、 满足 ，求 和 的值.
方法一：解方程组，分别求出 、 的值，代入代数式求值；
方法二：仔细观察两个方程中未知数的系数之间的关系，通过适当变形整体求代数式的值.解法如下：
①－②，得： ；①＋②×2，得： .
比较：方法一运算量较大，是常规思路；方法二运算较为简单，这种解题思路就是通常所说的“整体思想”.
（问题解决）
(1)、已知二元一次方程组 ，则 ； .(2)、某班级因组织活动购买奖品.买13支铅笔、4块橡皮、2本笔记本共需48元；买25支铅笔、7块橡皮、3本笔记本共需84元.则购买5只铅笔、5块橡皮、5本笔记本共需元.(3)、对于实数 、 ，定义新运算： ，其中 、 、 是常数，等式右边是通常的加减法和乘法运算.已知 ， ，那么 的值是.