2022年初中数学浙教版七年级下册2.4二元一次方程的应用能力阶梯训练——容易版

试卷更新日期：2022-01-24 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，直线 $a / / b$ ，∠1的度数比∠2的度数大56°，若设 $∠ 1 = x °$ ， $∠ 2 = y °$ ，则可得到的方程组为（）

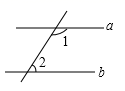A、 ${\begin{array}{l} x = y - 56 \\ x + y = 180 \end{array}$ B、 ${\begin{array}{l} x = y + 56 \\ x + y = 180 \end{array}$ C、 ${\begin{array}{l} x = y - 56 \\ x + y = 90 \end{array}$ D、 ${\begin{array}{l} x = y + 56 \\ x + y = 90 \end{array}$

查看试题解析
2. 甲、乙两水池现共贮水40 t，如果甲池进水4 t，乙池进水8 t，那么甲池水量等于乙池水量，则甲、乙两水池原先各自的贮水量是（）

A、甲22t，乙18t B、甲23t，乙17t C、甲21t，乙19t D、甲24t，乙16t

查看试题解析
3. 某市举办中学生足球赛，按比赛规则，每场比赛都要分出胜负，胜1场得3分，负一场扣1分，菁英中学队在8场比赛中得到12分，若设该队胜的场数为x负的场数为y，则可列方程组为（）

A、 ${\begin{cases} x - y = 8 ， \\ 3 x - y = 12 \end{cases}$ B、 ${\begin{cases} x + y = 18 ， \\ 3 x + y = 12 \end{cases}$ C、 ${\begin{cases} x + y = 8 ， \\ 3 x - y = 12 \end{cases}$ D、 ${\begin{cases} x - y = 8 ， \\ 3 x + y = 12 \end{cases}$

查看试题解析
4. 甲、乙两人做同样的零件，如果甲先做1天，乙再开始做，5天后两人做的一样多；如果甲先做30个，乙再开始做，4天后乙反而比甲多做10个。甲、乙两人每天分别做多少个？设甲每天做x个，乙每天做y个，则列出的方程组是（）

A、 ${\begin{cases} 6 x = 5 y \\ 30 + 4 x = 4 y + 10 \end{cases}$ B、 ${\begin{cases} 1 + 5 x = 6 y \\ 30 + 4 x = 4 y - 10 \end{cases}$ C、 ${\begin{cases} 6 x = 5 y \\ 30 + 4 x = 4 y - 10 \end{cases}$ D、 ${\begin{cases} 1 + 5 x = 5 y \\ 30 + 4 x = 4 y + 10 \end{cases}$

查看试题解析
5. 《九章算术》有题如下：“仅有五雀、六燕，集称之衡，雀俱重，燕俱轻，一雀一燕交而处，衡适平.并燕、雀重一斤.问燕、雀一枚各重几何？”意思是：今有5只雀、6只燕，分别聚集而用衡器称之，聚在一起的雀重、燕轻，将1只雀、1只燕交换位置而放，重量相同.5只雀、6只燕重量为1斤.问燕雀每只各重多少？（注：古代1斤＝16两）若设每只雀、燕分别重 $x$ 两、 $y$ 两，则可列方程组为（）

A、 ${\begin{array}{l} 4 x + y = 5 y + x, \\ 5 x + 6 y = 16. \end{array}$ B、 ${\begin{array}{l} 5 x + y = 6 y + x, \\ 5 x + 6 y = 16. \end{array}$ C、 ${\begin{array}{l} 4 x - y = 5 y - x, \\ 5 x + 6 y = 16. \end{array}$ D、 ${\begin{array}{l} 5 x - y = 6 y - x, \\ 5 x + 6 y = 16. \end{array}$

查看试题解析

二、填空题

6. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重．问：每只雀、燕的重量各为多少？设一只雀的重量为 $x$ 斤，一只燕的重量为 $y$ 斤，则可列方程为．

查看试题解析
7. 鸡兔同笼共9只，腿26条，则鸡只，兔只．

查看试题解析
8. 《算法统宗》是中国古代数学名著，作者是明代数学家程大位．其中有一个“绳索量竿”问题：“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托，问索长几尺”．
译文：现有一根杆和一条绳索，用绳索去量杄，绳索比杆子长5尺；如果将绳索对折后再去量竿，就比竿子短5尺，问绳索长几尺？注：一托 $= 5$ 尺

设绳索长X尺，竿子长y尺，依题意，可列方程组为．

查看试题解析
9. 一副三角板如图方式摆放，且∠1的度数比∠2的度数大50°，设 $∠ 1 = x^{°} ， ∠ 2 = y^{°}$ ，则可得关于x，y的方程组为.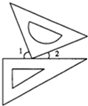

查看试题解析
10. 一片草原上的一片青草，到处长的一样密、一样快.20头牛在96天可以吃完，30头牛在60天可以吃完，则70头牛吃完这片青草需天.

查看试题解析

三、综合题

11. 为提高饮水质量，越来越多的居民选购家用净水器．一商场抓住商机，从厂家购进了A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元．

(1)、求A、B两种型号家用净水器各购进了多少台

(2)、为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元．（注：毛利润=售价﹣进价）

查看试题解析
12. 光明中学八年级师生共466人准备参加社会实践活动，现预备了49座和37座两种客车共10辆，刚好坐满．已知37座客车租金为每辆700元，49座客车为每辆1200元，问：

(1)、49座和37座两种客车各租了多少辆？

(2)、若租用同种客车，要使每位师生都有座位，应该怎么租用才合算？

查看试题解析

13. 为改善生态环境，美化居住环境，我市园林管理部门计划在沂河两岸种植水杉树．现甲、乙两家林场有相同的水杉树苗可供选择，具体销售方案如下：

甲林场		乙林场
购树苗数量	销售单价	购树苗数量	销售单价
不超过1000棵	4元	不超过2000棵	4元
超过1000棵的部分	3.8元	超过2000棵的部分	3.6元

设购买水杉树苗 $x$ 棵，到两家林场购买所需费用分别为 $y_{甲}$ 元， $y_{乙}$ 元．

(1)、该村需要购买1500棵水杉树苗，若都在甲林场购买，所需费用为元，若都在乙林场购买所需费用为元；

(2)、当

x > 2000

时，分别求出

y_{甲}

，

y_{乙}

与

x

之间的函数关系式；

(3)、如果你是我市园林管理部门的负责人，选择到哪家林场购买树苗合算?为什么?

查看试题解析

2022年初中数学浙教版七年级下册2.4二元一次方程的应用 能力阶梯训练——容易版

一、单选题

二、填空题

三、综合题

2022年初中数学浙教版七年级下册2.4二元一次方程的应用能力阶梯训练——容易版