2021-2022学年浙教版数学八下2.3 一元二次方程的应用 同步练习
试卷更新日期：2022-01-24 类型：同步测试
一、单选题
-
1. 某品牌足球2020年单价为200元，到2022年后，公司将该品牌足球的单价确定为162元，则2020年到2022年该品牌足球单价平均每年降低的百分率是（ ）A、10% B、19% C、20% D、30%2. 某商场在销售一种日用品时发现，如果以单价20元销售，则每周可售出100件，若销售单价每提高0.5元，则每周销售量会相应减少2件．如果该商场这种日用品每周的销售额达到2024元．若设这种日用品的销售单价为x元，则根据题意所列方程正确的是（ ）A、（20+x）（100﹣2x）＝2024 B、（20+x）（100﹣）＝2024 C、x[100﹣2（x﹣20）]＝2024 D、x（100﹣×2）＝20243. 某超市一月份的营业额为36万元，由于受疫情影响，二月份营业额有所下降，三月份开始复苏，营业额为48万元，设从一月到三月平均每月的增长率为x，则下面所列方程正确的是（ ）A、 B、 C、 D、4. 《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔不及长一十二步，问阔及长各几步？”译文：“一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽各是多少步？”若设矩形田地的长为x步，则可列方程为（ ）A、2x+2（x+12）＝864 B、2x+2（x﹣12）＝864 C、x（x+12）＝864 D、x（x﹣12）＝8645. 某口罩生产厂家2019年产量为100万个，为支持防疫工作，加大生产，2021年口罩产量为196万个，求该口罩厂家产量的年平均增长率．设该口罩厂家产量的年平均增长率为x，则根据题意可列方程为（ ）A、100x2＝196 B、100（1﹣x）2＝196 C、196（1＋x）2＝100 D、100（1＋x）2＝1966. 如图所示，A，B，C，D为矩形的四个顶点，AB=16cm，AD=8cm，动点P，Q分别从点A，C同时出发，点P以3cm/s的速度向B移动，一直到达B为止；点Q以2cm/s的速度向D移动．当P，Q两点从出发开始几秒时，点P和点Q的距离是10cm．(若一点到达终点，另一点也随之停止运动)（ ）
A、2s或s B、1s或s C、s D、2s或s7. 为积极推进“互联网+享受教育”课堂生态重构，加强对学校教育信息化的建设的投入，已知2021年计划投入1000万元，预计到2023年需投入1440万元，设投入经费的年平均增长率为x，根据题意，下面所列方程正确的是（ ）A、1000（1+x）2＝1440 B、1000（1+2x）＝1440 C、1000+1000x+1000x2＝1440 D、1000（x2+1）＝14408. “科学务农，前景广阔”，虎林市农民王大哥在进行水稻旱种后喜获丰收，两年经过两次连续增产，由原来的亩产量10百斤上涨为现在的14.4百斤，设平均每次增产的百分比为x，则可列方程（ ）A、 B、 C、 D、9. 电影《长津湖》上映以来，全国票房连创佳绩．据不完全统计，某市第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达18亿元，将增长率记作x，则方程可以列为（ ）A、2+2x+2x2＝18 B、2（1+x）2＝18 C、（1+x）2＝18 D、2+2（1+x）+2（1+x）2＝1810. 某渔具店销售一种鱼饵，每包成本价为10元，经市场调研发现：售价为20元时，每天可销售40包，售价每上涨1元，销量将减少3包．如果想获利408元，设这种鱼饵的售价上涨x元，根据题意可列方程为（ ）A、（20+x）（40﹣3x）＝408 B、（x﹣10）[40﹣3（x﹣20）]＝408 C、（20+x﹣10）（40﹣3x）＝408 D、（20+x）（40﹣3x）﹣10×40＝408二、填空题
-
11. 智能音箱是市场上最火的智能产品之一，某商户一月份销售了100个智能音箱，三月份比一月份多销售44个，设该公司二、三月销量的月平均增长率为x，则可列方程为 ．12. 如图，学校课外生物小组的试验园地的形状是长35米、宽20米的矩形．为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为660平方米，则小道的宽为多少米？若设小道的宽为x米，则根据题意，列方程为 ．
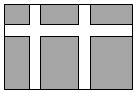13. 如图，在长为32米，宽为20米的矩形地面上：修建如图所示的道路（图中的阴影部分），余下部分铺设草坪，要使得草坪的面积为540平方米，则可列方程为 ．
14. 某厂家2020年1~5月份的口罩产量统计如图所示，设从2月份到4月份，该厂家口罩产量的月平均增长率为 ，根据题意可得方程 ．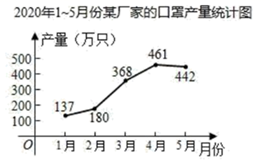
15. 将进货单价为40元的商品按50元出售时，就能卖出500个，已知这种商品每个涨价1元，其销售量就减少10个，为了赚得8000元的利润，商品售价应为元．16. 某超市销售一种饮料，平均每天可售出100箱，每箱利润20元.为扩大销售，超市准备适当降价.据测算，每箱每降价4元，平均每天可多售出20箱.若要使每天销售这种饮料获利1280元，每箱应降价多少元？设每箱降价x元，可列方程.三、综合题
-
17. 去年某商店第一季度营业额为120万元，第二季度的营业额比第一季度增长了25%，第三、第四季度营业额的增长率相同，且第四季度的营业额为216万元．
求：
(1)、该店第二季度的营业额；(2)、该店第三、第四季度营业额的增长率．18. 2020年，受新冠肺炎疫情影响．口罩紧缺，某网店购进了一批口罩，二月份销售了256袋，三、四月该口罩十份畅销，销售量持续走高，四月份的销售量达到400袋．(1)、求三、四这两个月销售量的月平均增长率；(2)、如果继续按照相同的增长率增长，那么五月份的销售量会达到多少袋口罩？19. 如图是一张长20cm、宽13cm的矩形纸板，将纸板四个角各剪去一个边长为xcm的正方形，然后将四周突出部分折起，可制成一个无盖纸盒
(1)、这个无盖纸盒的长为cm，宽为cm （用含x的式子表示）(2)、若要制成一个底面积是144cm2的无盖长方体纸盒，求x的值20. 水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．(1)、若将这种水果每斤的售价降低x元，则每天的销售量是 斤。（用含x的代数式表示）(2)、销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？21. 某餐馆推出特色小吃，推出了“堂食”和“外卖”两种销售方式．当特色小吃以“外卖”方式售出时，餐馆需额外支付网络平台服务费，服务费为“外卖”销售额的20%．（注：收入＝销售额﹣服务费）根据以上信息，解决下列问题：
(1)、10月份，该餐馆需额外支付的服务费为元，该月收入为元；(2)、经调研，该餐馆在10月份“堂食”600份销量的基础上，“堂食”价格每提高1元，“堂食”的销量就减少5份，但提高后的价格不能超过30元/份；“外卖”价格始终保持不变．该餐馆计划11月份只做800份特色小吃，预计全部售完．问“堂食”如何定价，11月份的收入是10760元？22. 某商场计划购进一批书包，市场调查发现：当某种进货价格为30元的书包以40元的价格出售时，平均每月售出600个，并且书包的售价每提高1元，每月销售量就减少10个.(1)、当售价定为42元时，每月可售出个；(2)、若书包的月销售量为300个，则每个书包的定价为元；(3)、当商场每月获得10000元的销售利润时，为体现“薄利多销”的销售原则，你认为销售价格应定为多少元？23. 2020年春节期间，新型冠状病毒肆虐，突如其来的疫情让大多数人不能外出，网络销售成为这个时期最重要的一种销售方式.某乡镇贸易公司因此开设了一家网店，销售当地某种农产品.已知该农产品成本为每千克10元.调查发现，每天销售量与销售单价(元)满足如图所示的函数关系(其中).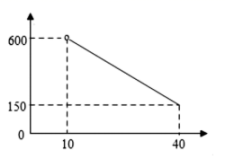
(1)、写出与之间的函数关系式.(2)、当销售单价为多少元时，每天的销售利润可达到6000元？24. 山水旅行社的一则广告如下：我社组团去A风景区旅游，收费标准为：如果人数不超过30人，人均旅游费用为800元；如果人数多于30人，那么每增加1人，人均旅游费用降低10元，但人均旅游费用不得低于500元，某公司组织一批员工到A风景区旅游，支付给旅行社28000元.(1)、该公司的人数_30人（填“大于、小于或等于”）(2)、如果设该公司的人数为x，用含x的代数式表示人均旅游费用_（填化简结果）(3)、求（2）中的x.25. 某商店销售一款进价为80元的童装，每件售价为120元时，每天可售出20件．为了尽快减少库存，商店决定降价销售，经市场调查发现，该童装每降价1元，每天可多售出2件．(1)、每件童装售价定为多少元时，该商店每天销售这款童装的总利润为1200元？(2)、该商店每天销售这款童装的总利润能达到1300元吗？若能，求出此时的售价，若不能，请说明理由．26. 因国家对新能源的支持以及各种利好因素的影响，某新能源企业的利润逐年提高，据统计，该企业2018年的利润为3亿元，2020年的利润为4.32亿元．(1)、求该企业从2018年到2020年利润的年平均增长率；(2)、若保持前两年利润的年平均增长率不变，该企业2021年的利润能否超过5亿元？