2021-2022学年浙教版数学八下1.2 二次根式的性质同步练习

试卷更新日期：2022-01-24 类型：同步测试

进入出卷网下载

一、单选题

1. 把代数式 $(a - 1) \sqrt{\frac{1}{1 - a}}$ 中的 $a - 1$ 移到根号内，那么这个代数式等于（）

A、 $- \sqrt{1 - a}$ B、 $\sqrt{a - 1}$ C、 $\sqrt{1 - a}$ D、 $- \sqrt{a - 1}$

查看试题解析
2. 如果 $a b > 0$ ， $a + b < 0$ ，那么下面各式不正确的是（）

A、 $\sqrt{a^{2}} = - a$ B、 $\sqrt{\frac{a}{b}} \times \sqrt{\frac{b}{a}} = 1$ C、 $\sqrt{a b} \div \sqrt{\frac{a}{b}} = - b$ D、 $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$

查看试题解析
3. 下列根式中是最简二次根式是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{\frac{4}{7}}$ C、 $\sqrt{12}$ D、 $\sqrt{2}$

查看试题解析
4. 二次根式 $\sqrt{a}$ (a≥0)是（）

A、正数 B、负数 C、0 D、非负数

查看试题解析
5. 若二次根式 $\sqrt{3 n}$ 的值是整数，则下列n的取值不符合条件的是（）

A、n=3 B、n=12 C、n=18 D、n=27

查看试题解析
6. 下列二次根式中，最简二次根式（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.7}$ C、 $\sqrt{8}$ D、 $\sqrt{x^{2} + 1}$

查看试题解析
7. 下列各式中，正确的是（）

A、 $\sqrt{36} = \pm 6$ B、 $\pm \sqrt{25} = \pm 5$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt[3]{- 27} = 3$

查看试题解析
8. 已知 $a > 0$ ，那么 $\sqrt{- \frac{4 a}{b}}$ 可化简为（）

A、 $2 b \sqrt{- a b}$ B、 $- \frac{2}{b} \sqrt{a b}$ C、 $- \frac{2}{b} \sqrt{- a b}$ D、 $\frac{2}{b} \sqrt{- a b}$

查看试题解析
9. 下列四个等式：① $\sqrt{{(- 4)}^{2}} = - 4$ ；② ${(- \sqrt{4})}^{2} = 16$ ；③ ${(- \sqrt{4})}^{2} = 4$ ；④ ${(\sqrt{4})}^{2} = 4$ ．正确的是（）

A、①② B、②④ C、③④ D、①③

查看试题解析
10. 下列计算正确的是（）

A、 $\sqrt{4}$ ＝±2 B、 $\sqrt{36}$ ＝6 C、 $\sqrt{{(- 6)}^{2}}$ ＝﹣6 D、﹣ $\sqrt[3]{- 8}$ ＝﹣2

查看试题解析

二、填空题

11. 实数 $a$ 在数轴上的位置如下图所示，化简 $\sqrt{a^{2}} - a$ 等于

查看试题解析
12. 计算： $\sqrt{{(π - 4)}^{2}}$ ＝（计算结果保留π）．

查看试题解析
13. 化简： $\sqrt{16 a^{2} b}$ （a＜0）＝．

查看试题解析
14. 化简： $\sqrt{{(2 - \sqrt{5})}^{2}} =$

查看试题解析
15. 已知1＜a＜3，则化简 $\sqrt{1 - 2 a + a^{2}}$ ﹣ $\sqrt{a^{2} - 8 a + 16}$ 的结果是．

查看试题解析
16. 实数a，b在数轴上的位置如图所示，则化简 $| a + b | - \sqrt{{(b - a)}^{2}}$ ．

查看试题解析

三、综合题

17.

(1)、已知二次根式 $\sqrt{3 - \frac{1}{2} x}$ ，求x的取值范围；

(2)、当x=-2时，求二次根式 $\sqrt{3 - \frac{1}{2} x}$ 的值；

(3)、若二次根式 $\sqrt{3 - \frac{1}{2} x}$ 的值为1，求x的值．

查看试题解析
18. 当x分别取下列值时，求二次根式 $\sqrt{9 - 8 x}$ 的值．

(1)、x=0；

(2)、x= $\frac{1}{2}$ ；

(3)、x= -2．

查看试题解析
19. 阅读材料：把根式 $\sqrt{x \pm 2 \sqrt{y}}$ 进行化简，若能找到两个数 $m$ ， $n$ ，使 $m^{2} + n^{2} = x$ 且 $m n = \sqrt{y}$ ，则把 $x \pm 2 \sqrt{y}$ 变成 $m^{2} + n^{2} \pm 2 m n = {(m \pm n)}^{2}$ 开方，从而使得 $\sqrt{x \pm 2 \sqrt{y}}$ 化简.
例如：化简 $\sqrt{3 + 2 \sqrt{2}}$ .

解： $∵ 3 + 2 \sqrt{2} = 1 + 2 + 2 \sqrt{2} = 1^{2} + {(\sqrt{2})}^{2} + 2 \times 1 \times \sqrt{2} = {(1 + \sqrt{2})}^{2}$ ，

$∴$ $\sqrt{3 + 2 \sqrt{2}} = \sqrt{{(1 + \sqrt{2})}^{2}} = 1 + \sqrt{2}$ .

请你仿照上面的方法，化简下列各式：

(1)、 $\sqrt{7 + 4 \sqrt{3}}$ ；

(2)、 $\sqrt{5 - 2 \sqrt{6}}$ .

查看试题解析
20. 实践与探索

(1)、填空： $\sqrt{3^{2}} =$ ； $\sqrt{{(- 5)}^{2}} =$ ．

(2)、观察第（1）的结果填空：当 $a \geq 0$ 时， $\sqrt{a^{2}} =$ ；当 $a < 0$ 时， $\sqrt{a^{2}} =$ ．

(3)、利用你总结的规律计算： $\sqrt{{(x - 2)}^{2}} + \sqrt{{(x - 4)}^{2}}$ ，其中x的取值范围在数轴上表示为．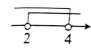

查看试题解析
21. 已知：实数a，b满足 $\sqrt{a + 3} + {(b - 4)}^{2} = 0$ ．

(1)、可得 $a =$ ， $b =$ ；

(2)、当一个正实数x的两个平方根分别为 $m + a$ 和 $b - 2 m$ 时，求x的值．

查看试题解析
22. 阅读下列解题过程
例：若代数式 $\sqrt{{(a - 1)}^{2}} + \sqrt{{(a - 3)}^{2}}$ 的值是2，求a的取值范围．

解：原式＝|a﹣1|+|a﹣3|，

当a＜1时，原式＝（1﹣a）+（3﹣a）＝4﹣2a＝2，解得a＝1（舍去）；

当1≤a≤3时，原式＝（a﹣1）+（3﹣a）＝2＝2，符合条件；

当a＞3时，原式＝（a﹣1）+（a﹣3）＝2a﹣4＝2，解得a＝3（舍去）

所以，a的取值范围是1≤a≤3

上述解题过程主要运用了分类讨论的方法，请你根据上述理解，解答下列问题

(1)、当2≤a≤5时，化简： $\sqrt{{(a - 2)}^{2}} + \sqrt{{(a - 5)}^{2}}$ ＝ 3 ；

(2)、若等式 $\sqrt{{(3 - a)}^{2}} + \sqrt{{(a - 7)}^{2}}$ ＝4成立，则a的取值范围是 3≤a≤7 ；

(3)、若 $\sqrt{{(a + 1)}^{2}} + \sqrt{{(a - 5)}^{2}}$ ＝8，求a的取值．

查看试题解析
23. 求代数式 $a + \sqrt{1 - 2 a + a^{2}}$ 的值，其中 $a = 1007$ ．
如图是小亮和小芳的解答过程：

(1)、的解法是错误的；

(2)、错误的原因在于未能正确的运用二次根式的性质：；

(3)、求代数式 $a + 2 \sqrt{a^{2} - 6 a + 9}$ 的值，其中 $a = - 2020$

查看试题解析
24. 在平面直角坐标系中，点A（0，a），B（b，0）的坐标满足|a＋b﹣6|＋ $\sqrt{a - b + 2}$ ＝0

(1)、求点A、B的坐标；

(2)、如图1，将AB平移到CD，点A对应点C（﹣2，m），若△ABC面积为12，连接CO，求点C的坐标；

(3)、如图2，将AB平移到CD，若点C、D也在坐标轴上，点F为线段AB上一点且∠BOF＝20°，FP平分∠BFO，CP平分∠BCD，FP与CP交于点P．求∠P的度数．

查看试题解析
25. 有这样一类题目：将 $\sqrt{a \pm 2 \sqrt{b}}$ 化简，如果你能找到两个数m、n，使m²＋n²＝a 且mn＝ $\sqrt{b}$ ，则a±2 $\sqrt{b}$ 将变成m²＋n²±2mn，即变成(m±n)² ，从而使 $\sqrt{a \pm 2 \sqrt{b}}$ 得以化简．例如，因为5＋2 $\sqrt{6}$ ＝3＋2＋2 $\sqrt{6}$ ＝( $\sqrt{3}$ )²＋( $\sqrt{2}$ )²＋2 $\sqrt{2}$ × $\sqrt{3}$ ＝( $\sqrt{3}$ ＋ $\sqrt{2}$ )² ，所以 $\sqrt{5 + 2 \sqrt{6}}$ ＝ $\sqrt{{(\sqrt{3} + \sqrt{2})}^{2}} = \sqrt{3} + \sqrt{2}$ ．
请仿照上面的例子化简下列根式：

(1)、 $\sqrt{4 + 2 \sqrt{3}}$

(2)、 $\sqrt{9 - 4 \sqrt{5}}$

查看试题解析