2022年初中数学浙教版七年级下册第一章平行线 章末检测——普通版
试卷更新日期:2022-01-23 类型:单元试卷
一、单选题
-
1. 如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
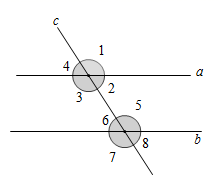 A、∠3=∠5 B、∠4=∠7 C、∠2+∠3=180° D、∠1=∠32. 如图,给出下列条件:①∠1=∠2:②∠3=∠4:③AB∥CE,且∠ADC=∠B:④AB∥CE,且∠BCD=∠BAD.其中能推出BC∥AD的条件为( )
A、∠3=∠5 B、∠4=∠7 C、∠2+∠3=180° D、∠1=∠32. 如图,给出下列条件:①∠1=∠2:②∠3=∠4:③AB∥CE,且∠ADC=∠B:④AB∥CE,且∠BCD=∠BAD.其中能推出BC∥AD的条件为( ) A、①② B、②④ C、②③ D、②③④3. 如图,点 在 的延长线上,下列条件不能判断 的是( )
A、①② B、②④ C、②③ D、②③④3. 如图,点 在 的延长线上,下列条件不能判断 的是( ) A、 B、 C、∠5=∠B D、4. 如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A、 B、 C、∠5=∠B D、4. 如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.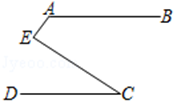 A、70 B、150 C、90 D、1005. 如图, 沿射线 方向平移到 (点E在线段 上),如果 , ,那么平移距离为( )
A、70 B、150 C、90 D、1005. 如图, 沿射线 方向平移到 (点E在线段 上),如果 , ,那么平移距离为( )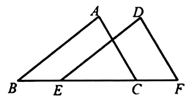 A、3cm B、5cm C、8cm D、13cm6. 如图,已知直线 , , ,则 等于( )
A、3cm B、5cm C、8cm D、13cm6. 如图,已知直线 , , ,则 等于( )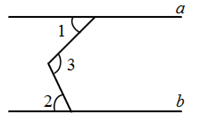 A、110° B、100° C、130° D、120°7. 下列说法中:①40°35′=2455′;②如果∠A+∠B=180°,那么∠A与∠B互为余角;③经过两点有一条直线,并且只有一条直线;④在同一平面内,不重合的两条直线不是平行就是相交.正确的个数为( ).A、1个 B、2个 C、3个 D、4个8. 如图,AB//CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( )
A、110° B、100° C、130° D、120°7. 下列说法中:①40°35′=2455′;②如果∠A+∠B=180°,那么∠A与∠B互为余角;③经过两点有一条直线,并且只有一条直线;④在同一平面内,不重合的两条直线不是平行就是相交.正确的个数为( ).A、1个 B、2个 C、3个 D、4个8. 如图,AB//CD,∠FGB=154°,FG平分∠EFD,则∠AEF的度数等于( )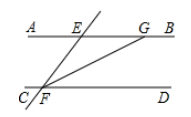 A、26° B、52° C、54° D、77°9. 某同学的作业如下框,其中※处填的依据是( )
A、26° B、52° C、54° D、77°9. 某同学的作业如下框,其中※处填的依据是( )如图,已知直线 .若 ,则 .
请完成下面的说理过程.
解:已知 ,
根据(内错角相等,两直线平行),得 .
再根据( ※ ),得 .
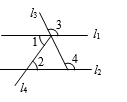 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补10. 下列说法正确的有( )个
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补10. 下列说法正确的有( )个①同位角相等;
②一条直线有无数条平行线;
③在同一平面内,两条不相交的线段是平行线;
④如果 , ,则 ;
⑤过一点有且只有一条直线与已知直线平行.
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 如图,已知OC平分∠AOB,CD//OB,若OD=3cm,则CD=cm.
 12. 如图,已知直线EF⊥MN垂足为F , 且∠1=138°,则当∠2等于 时,AB∥CD .
12. 如图,已知直线EF⊥MN垂足为F , 且∠1=138°,则当∠2等于 时,AB∥CD . 13. 如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是 .
13. 如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是 . 14. 已知 ∠1的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为 .15. 如图,AB//CD , ∠A=25° , ∠E=80°,则∠C的度数是 .
14. 已知 ∠1的两边分别平行于 ∠2 的两边,若 ∠1 = 40°,则 ∠2 的度数为 .15. 如图,AB//CD , ∠A=25° , ∠E=80°,则∠C的度数是 . 16. 高兴同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP=°.
16. 高兴同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP=°.
三、解答题
-
17. 如图, ,直线 分别交 , 于E、F两点,且 平分 , ,求 的度数.
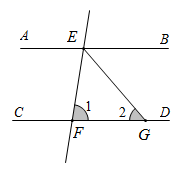 18. 已知:∠DEC+∠C=180°,DE平分∠ADF , ∠F=∠1.求证:∠B=∠C .
18. 已知:∠DEC+∠C=180°,DE平分∠ADF , ∠F=∠1.求证:∠B=∠C .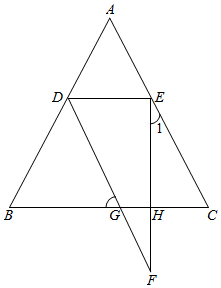 19. 已知:在三角形ABC和三角形DEF中,AB∥DE .
19. 已知:在三角形ABC和三角形DEF中,AB∥DE . (1)、如图1,若三角形DEF的顶点F在三角形ABC的边AB上,且DF∥AC .
(1)、如图1,若三角形DEF的顶点F在三角形ABC的边AB上,且DF∥AC .求证:∠A=∠D;
(2)、如图2,若三角形DEF的顶点F在三角形ABC的内部,∠A=∠D , 则DF与AC有怎样的位置关系?请说明理由.20. 如图:网格图中小方格都是边长为1个单位长度的小正方形,已知三角形ABC的三个顶点都在网格的格点上,按要求完成下列各小题. (1)、请在图中画出将三角形ABC先向上平移1个单位长度,再向右平移3个单位长度后的图形,即三角形A′B′C′,并指出图中相等的线段;(2)、在(1)的基础上,A′B′,B′C′分别与AC交于点E,F.若∠A=50°,∠C′=51°,分别求出∠A′EF与∠B′FC的度数.21. 如图,已知AM//BN,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)、请在图中画出将三角形ABC先向上平移1个单位长度,再向右平移3个单位长度后的图形,即三角形A′B′C′,并指出图中相等的线段;(2)、在(1)的基础上,A′B′,B′C′分别与AC交于点E,F.若∠A=50°,∠C′=51°,分别求出∠A′EF与∠B′FC的度数.21. 如图,已知AM//BN,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.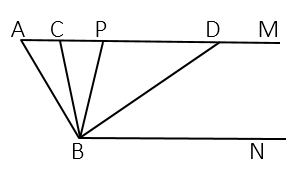 (1)、①当∠A=50°时,∠ABN的度数是;
(1)、①当∠A=50°时,∠ABN的度数是;②∵AM //BN,∴∠ACB=∠;
(2)、当∠A=x°,求∠CBD的度数(用x的代数式表示);(3)、当点P运动时,∠ADB与∠APB的度数之比是否随点P的运动而发生变化?若不变化,请求出这个比值;若变化,请写出变化规律.(4)、当点P运动到使∠ACB=∠ABD时,请直接写出2∠DBN 的度数.22. 小明同学遇到这样一个问题:
如图①,已知:AB∥CD,E为AB、CD之间一点,连接BE,ED,得到∠BED.
求证:∠BED=∠B+∠D.
小亮帮助小明给出了该问的证明.
证明:
过点E作EF∥AB
则有∠BEF=∠B
∵AB∥CD
∴EF∥CD
∴∠FED=∠D
∴∠BED=∠BEF+∠FED=∠B+∠D
请你参考小亮的思考问题的方法,解决问题:
(1)、直线l1∥l2 , 直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,猜想:如图②,若点P在线段CD上,∠PAC=15°,∠PBD=40°,求∠APB的度数.(2)、拓展:如图③,若点P在直线EF上,连接PA、PB(BD<AC),直接写出∠PAC、∠APB、∠PBD之间的数量关系.23. 已知点C在射线OA上.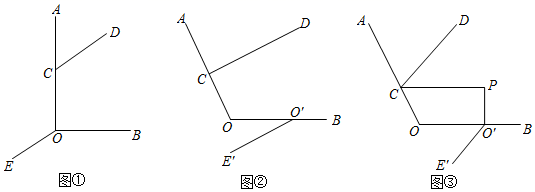 (1)、如图①,CD OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示)(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.24. 如图,政府规划由西向东修一条公路.从A修至B后为了绕开村庄,改为沿南偏东25°方向修建BC段,在C处又改变方向修建CD段,测得∠BCD=70°,在D处继续改变方向,朝与出发时相同的方向修至E.
(1)、如图①,CD OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示)(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.24. 如图,政府规划由西向东修一条公路.从A修至B后为了绕开村庄,改为沿南偏东25°方向修建BC段,在C处又改变方向修建CD段,测得∠BCD=70°,在D处继续改变方向,朝与出发时相同的方向修至E. (1)、补全施工路线示意图,求∠CDE的度数;(2)、原计划在AB的延长线上依次修建两个公交站M,N(均在CD右侧),连结DM和MN,求∠CDM与∠DMN的数量关系.
(1)、补全施工路线示意图,求∠CDE的度数;(2)、原计划在AB的延长线上依次修建两个公交站M,N(均在CD右侧),连结DM和MN,求∠CDM与∠DMN的数量关系.