2022年初中数学浙教版七年级下册第一章平行线 章末检测——容易版
试卷更新日期：2022-01-23 类型：单元试卷
一、单选题
-
1. 在如图所示的四个汽车标识图案中，能用平移变换来分析其形成过程的是（ ）A、
B、
C、
D、
2. 如图，∠1与∠2是同位角的是（ ）
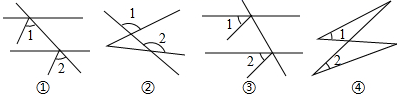A、①③ B、①② C、②③ D、③④3. 如图，下列说法不正确的是（ ）
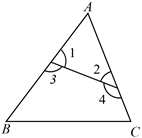A、 和 是同旁内角 B、 和 是内错角 C、 和 是同位角 D、 和 是同旁内角4. 下列说法正确的是（ ）A、相等的两个角是对顶角 B、同旁内角互补 C、平移前后的两个图形周长相等，面积相等 D、直线外一点到这条直线的垂线段叫做点到直线的距离5. 如图， ， 平分 交 于点 ，若 ，则 度数为（ ）
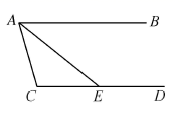A、 B、 C、 D、6. 如图，直线a∥b∥c，直角三角板的直角顶点落在直线b上，若∠1＝36°，则∠2等于（ ）
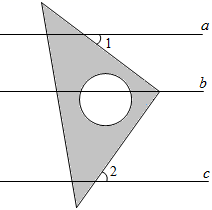A、36° B、44° C、54° D、64°7. 光线在不同介质中的传播速度不同，因此当光线从空气射向水中时，会发生折射．如图，在空气中平行的两条入射光线，在水中的两条折射光线也是平行的．若水面和杯底互相平行，且∠1＝122°，则∠2＝（ ）
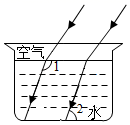A、61° B、58° C、48° D、41°8. 将一副直角三角板按如图方式摆放，若直线 ，则 的大小为（ ）
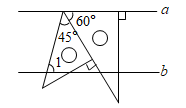A、 B、 C、 D、9. 如图 沿直线m向右平移 ，得到 ，下列说法错误的是（ ）
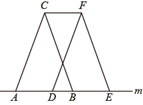A、 B、 C、 D、10. 如图所示，在下列四组条件中，能判定AB∥CD的是（ ）
A、∠1=∠2 B、∠BAD+∠ABC=180° C、∠3=∠4 D、∠ABD=∠BDC二、填空题
-
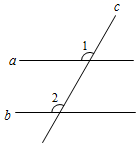
11. 如图，直线a，b被直线c所截，当∠1 ∠2时，a//b.（用“＞”，“＜”或“＝”填空）
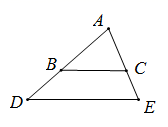
12. 如图，AB∥CD，CB平分∠ECD，若∠B＝26°，则∠1的度数是.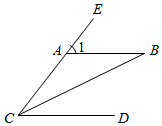
13. 如图，已知a∥b，∠1=110°，则∠2的度数是
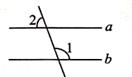14. 如图，直线a∥b，a与c相交于点A，过点A作直线c的垂线交b于点B.若∠1＝50°，则∠2的度数为.
15. 如图，直线 ， ， ，点 在直线 上， ，若 ，则 的度数为.
16. 如图所示， ，∠1=25°，则当 时， °.
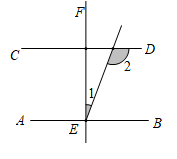
三、解答题
-
17. 如图，AD∥BE，∠1=∠2，求证：∠A=∠E.
请完成解答过程：
解：∵AD∥BE(已知)
∠A=∠()
又∵1=∠2(已知)
∴AC∥()
∴∠3=∠(两直线平行，内错角相等)
∴∠A=∠E()
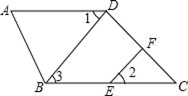
18. 如图，直线AB、CD相交于点O，且OE为∠BOC的平分线，DF∥OE，若∠AOC＝36°，求∠D的度数.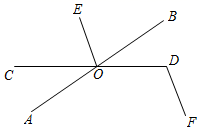
19. 如图，射线 平外 ，且 .求证： .
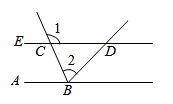20. 如图，在平面直角坐标系xOy中，已知三角形ABC三个顶点的坐标分别是A（4，3），B（3，1），C（1，2）.
(1)、在图中画出三角形ABC；(2)、将三角形ABC向左平移4个单位长度，在图5中画出平移后的三角形A1B1C1 ， 并分别写出点A1、B1、C1的坐标.21. 将两块大小相同的直角三角尺（即三角形 和三角形 ，其中 ，按如图所示的方式摆放（直角顶点 在斜边 上，直角顶点 在斜边 上），且 .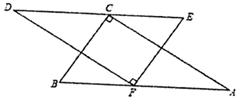
(1)、求 的度数；(2)、请你判断 与 是否平行，并说明理由.
