2022年初中数学浙教版八年级下册第二章一元二次方程章末检测——普通版

试卷更新日期：2022-01-22 类型：单元试卷

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 4 x - 6 = 0$ ，经过配方可变形为（）

A、 ${(x - 2)}^{2} = 10$ B、 ${(x - 2)}^{2} = 6$ C、 ${(x - 4)}^{2} = 6$ D、 ${(x - 2)}^{2} = 2$

查看试题解析
2. 下列配方正确的是（）

A、 $x^{2} + 2 x + 5 = {(x + 1)}^{2} + 6$ B、 $x^{2} + 3 x = {(x + \frac{3}{2})}^{2} - \frac{3}{2}$ C、 $3 x^{2} + 6 x + 1 = 3 {(x + 1)}^{2} - 2$ D、 $x^{2} - \frac{1}{2} x + \frac{3}{4} = {(x - \frac{1}{4})}^{2} + \frac{1}{16}$

查看试题解析
3. 若关于x的一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则 $a$ 的值是（）

A、1 B、－1 C、1或－1 D、0

查看试题解析
4. 下列关于 $x$ 的一元二次方程中，有两个不相等的实数根的方程是（）

A、 $x^{2} + 2 = 0$ B、 $2 x^{2} + 3 x + 2 = 0$ C、 $4 x^{2} - 12 x + 9 = 0$ D、 $3 x^{2} + 5 x - 8 = 0$

查看试题解析
5. 用配方法解方程ax²+bx+c＝0（a≠0），四个学生在变形时得到四种不同结果，其中配方正确的是（）

A、 ${(x + \frac{b}{2 a})}^{2} = \frac{4 a c - b^{2}}{4 a^{2}}$ B、 ${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{2 a^{2}}$ C、 ${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$ D、 ${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} + 2 a c}{2 a^{2}}$

查看试题解析
6. 已知一个等腰三角形的两边长恰是方程 $x^{2} - 6 x + 8 = 0$ 的两根，则这个等腰三角形的周长是（）

A、8 B、10 C、8或10 D、12

查看试题解析
7. 已知关于x的一元二次方程 $x^{2} - x + \frac{1}{4} m = 0$ 有两个不相等的实数根，设此方程的一个实数根为b，令 $y = 4 b^{2} - 4 b - 3 m + 3$ ，则（）

A、 $y > - 1$ B、 $y \geq - 1$ C、 $y \leq 1$ D、 $y < 1$

查看试题解析
8. 某公司计划用32m的材料沿墙（可利用）建造一个面积为120m²的仓库，设仓库中和墙平行的一边长为xm，则下列方程中正确的是（）

A、x（32﹣x）＝120 B、x（16﹣ $\frac{1}{2}$ x）＝120 C、x（32﹣2x）＝120 D、x（16﹣x）＝120

查看试题解析
9. 某市严格落实国家节水政策，2018年用水总量为6.5亿立方米，2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x，那么x满足的方程是（）

A、 $6.5 {(1 - x)}^{2} = 5.265$ B、 $6.5 {(1 + x)}^{2} = 5.265$ C、 $5.265 {(1 - x)}^{2} = 6.5$ D、 $5.265 {(1 + x)}^{2} = 6.5$

查看试题解析
10. 学校初二年级组织足球联赛，赛制为单循环制（每两个队之间比赛一场).共进行了 $28$ 场比赛，问初二年级有几个参赛班级？设初二年级有 $x$ 个班级参加比赛.根据题意列出方程正确的是（）

A、 $x^{2} = 28$ B、 $\frac{1}{2} x (x - 1) = 28$ C、 $\frac{1}{2} x^{2} = 28$ D、 $x (x - 1) = 28$

查看试题解析

二、填空题

11. 已知关于x的方程（x﹣1）²＝5﹣k没有实数根，那么k的取值范围是．

查看试题解析
12. 已知关于x的一元二次方程（m﹣3）x²﹣3x+m²＝9的常数项为0，则m的值为．

查看试题解析
13. 如果关于 $x$ 的方程 $x^{2} + (2 m - 1) x + m^{2} = 0$ 的根的判别式的值为 $5$ ，那么 $m =$ ．

查看试题解析
14. 若关于x的一元二次方程 $(m - 2) x^{2} + 3 x + m = 4$ 有一个根是0，则另一个根是．

查看试题解析
15. 某超市一月份的营业额为 $200$ 元，已知第一季度的营业额共 $728$ 万元，如果每月营业额的增长率为 $x$ ，根据题意，可列方程为．

查看试题解析
16. 已知正比例函数 $y = \frac{5}{13} x$ 图像上有一个点 $M$ ，点 $M$ 的横坐标是方程x²+6x﹣91＝0的根，则点 $M$ 的纵坐标为．

查看试题解析

三、解答题

17. 计算和解方程：

(1)、 $\sqrt{18}$ + $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{12}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ .

(2)、（ $\sqrt{5}$ ﹣ $\sqrt{2}$ ）（ $\sqrt{5}$ + $\sqrt{2}$ ）+（ $\sqrt{3}$ ﹣2）².

(3)、5x+2＝3x².

(4)、（2x﹣1）²＝（3x﹣4）².

查看试题解析
18. 已知：关于x的方程x²﹣（k+2）x+2k＝0．

(1)、求证：无论k取任何实数值，方程总有实数根．

(2)、若等腰三角形ABC的底边长为1，另两边的长恰好是这个方程的两个根，求 $△$ ABC的周长．

查看试题解析
19. 已知关于x的一元二次方程（a﹣3）x²﹣4x+3＝0

(1)、若方程的一个根为x＝﹣1，求a的值；

(2)、若方程有实数根，求满足条件的正整数a的值；

(3)、请为a选取一个合适的整数，使方程有两个整数根，并求这两个根．

查看试题解析
20. 已知点 $P (1 ， m)$ 、 $Q (n ， 1)$ 在反比例函数 $y = \frac{5}{x}$ 的图象上，直线 $y = k x + b$ 经过点 $P$ 、 $Q$ ，且与 $x$ 轴、 $y$ 轴的交点分别为 $A$ 、 $B$ 两点．

(1)、求直线 $P Q$ 的解析式；

(2)、 $O$ 为坐标原点，点 $D$ 在直线上（点 $C$ 与点 $B$ 不重合）， $A B = A C$ ，求点 $C$ 的坐标；

(3)、在（2）的条件下，点 $D$ 在坐标平面上，顺次联结点 $O$ 、 $B$ 、 $C$ 、 $D$ 的四边形 $O B C D$ 满足： $B C // O D$ ， $B O = C D$ ，求满足条件的点 $D$ 坐标．

查看试题解析
21. 某服装厂生产一批服装，2019年该类服装的出厂价是200元/件，2020年，2021年连续两年改进技术，降低成本，2021年该类服装的出厂价调整为162元/件．

(1)、这两年此类服装的出厂价下降的百分比相同，求平均下降率．

(2)、2021年某商场从该服装厂以出厂价购进若干件此类服装，以200元/件销售时，平均每天可销售20件．为了减少库存，商场决定降价销售．经调查发现，单价每降低5元，每天可多售出10件，如果每天盈利1150元，单价应降低多少元?

查看试题解析
22. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，尽快减少库存，增加利润.经市场调查发现，如果每件童装降价1元，那么平均可多售出2件.

(1)、设每件童装降价 $x$ 元时，每天可销售件，每件盈利元；（用 $x$ 的代数式表示）

(2)、为了扩大销售量，尽快减少库存，每件童装降价多少元时，平均每天赢利1200元；

(3)、平均每天赢利1300元，可能吗？请说明理由.

查看试题解析
23. 某农场要建一个饲养场（矩形ABCD），两面靠墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）.建成后木栏总长45米.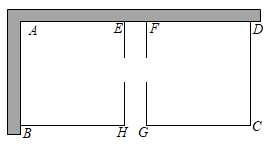

(1)、若饲养场（矩形ABCD）的一边CD长为8米，则另一边BC＝米.

(2)、若饲养场（矩形ABCD）的面积为180平方米，求边CD的长.

(3)、饲养场的面积能达到210平方米吗？若能达到，求出边CD的长；若不能达到，请说明理由.

查看试题解析
24. 科学研究表明接种疫苗是战胜新冠病毒的最有效途径.当前居民接种疫苗迎来高峰期，导致相应医疗物资匮乏，某工厂及时补进了一条一次性注射器生产线生产一次性注射器.开工第一天生产200万个，第三天生产288万个.试回答下列问题：

(1)、求前三天生产量的日平均增长率；

(2)、经调查发现，1条生产线最大产能是600万个/天，若每增加 $1$ 条生产线，每条生产线的最大产能将减少20万个/天.
①现该厂要保证每天生产一次性注射2600万个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

②是否能增加生产线，使得每天生产一次性注射器5000万个，若能，应该增加几条生产线？若不能，请说明理由.

查看试题解析

2022年初中数学浙教版八年级下册第二章一元二次方程 章末检测——普通版

一、单选题

二、填空题

三、解答题

2022年初中数学浙教版八年级下册第二章一元二次方程章末检测——普通版