2021-2022学年苏科版数学七年级下册8.3同底数幂的除法同步练习（培优）

试卷更新日期：2022-01-22 类型：同步测试

进入出卷网下载

一、单选题

1. 广阔无垠的太空中有无数颗恒星，其中离太阳系最近的一颗恒星称为“比邻星”，它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位，1光年约为9500000000000千米.则“比邻星”距离太阳系约为（）

A、 $4 \times 10^{13}$ 千米 B、 $4 \times 10^{12}$ 千米 C、 $9. 5 \times 10^{13}$ 千米 D、 $9. 5 \times 10^{12}$ 千米

查看试题解析
2. 已知a+2b-2=0，则2^a×4^b（）

A、4 B、8 C、24 D、32

查看试题解析
3. a^3m+1可以写成（）

A、(a³)m+1 B、(a^m)³+1 C、a·a^3m D、（ a^m）^2m+1

查看试题解析
4. 若3³×9^m=3¹¹ ，则m的值为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 若 $a = - {0.3}^{2} ， b = - 3^{- 2} ， c = {(- \frac{1}{3})}^{- 2} ， d = {(- \frac{1}{3})}^{0}$ ，则它们的大小关系是（）

A、a<b<c<d B、a<d<c<b C、b<a<d<c D、c<a<d<b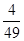

查看试题解析
6. 若 $3^{x} = 4$ ， $9^{y} = 7$ ，则 $3^{x - 2 y}$ =（）

A、 B、 $\frac{4}{7}$ C、 $\frac{3}{4}$ D、

查看试题解析
7. 计算 ${(\frac{2}{3})}^{2003} \times {1.5}^{2002} \times {(－ 1)}^{2004}$ 的结果是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $－ \frac{2}{3}$ D、 $－ \frac{3}{2}$

查看试题解析
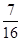8. 观察等式（2a﹣1）^a+2=1，其中a的取值可能是（）

A、﹣2 B、1或﹣2 C、0或1 D、1或﹣2或0

查看试题解析
9. 在：① ${(- 1)}^{0} = 1$ ，② ${(- 1)}^{1} = - 1$ ，③ $3 a^{- 2} = \frac{1}{3 a^{2}}$ ， ④ ${(- x)}^{5} \div {(- x)}^{3} = - x^{2}$ 中，其中正确的式子有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 将 $3^{﹣ 1} x （ x + y ）^{﹣}^{3}$ 写成只含有正整数指数幂的形式是（）

A、 $\frac{x}{3 x + y^{3}}$ B、 $\frac{x}{3 {(x + y)}^{3}}$ C、 $\frac{3 x}{x + y^{3}}$ D、 $\frac{3 x}{{(x + y)}^{3}}$

查看试题解析
11. 若 $x > 1$ ， $y > 0$ ，且满足 $x y = x^{y} ， \frac{x}{y} = x^{3 y}$ ，则 $x + y$ 的值为（）.

A、1 B、2 C、 $\frac{9}{2}$ D、 $\frac{11}{2}$

查看试题解析

二、填空题

12. 化简 ${(- 2 a^{- 3})}^{- 2} {(b c^{- 1})}^{3}$ = . （结果只含有正整数指数的形式）

查看试题解析
13. 若 ${(x + 2)}^{x - 1} = 1$ ，则 $x =$ .

查看试题解析
14. 根据数值转换机的示意图，输出的值为.

查看试题解析
15. 已知 10^x= 2， 10^y=3 ，则 $10^{2 x - y} =$ .

查看试题解析
16. 已知 $2^{2 m + 1} + 4^{m} = 48$ ，则 $m =$ .

查看试题解析
17. ${0.125}^{2019} \times {(- 8)}^{2020}$ =.若2•4^m•8^m=2²¹ ，则m=.

查看试题解析
18. 已知2x+5y﹣4＝0，则4^x×32^y＝.

查看试题解析
19. ${(- \frac{2}{3})}^{999}$ × ${(- 1.5)}^{1000}$ ＝．

查看试题解析

三、计算题

20. 已知 a^m=2， aⁿ=5， a^k=3 ，求 a^3m-2n+k的值.

查看试题解析
21.

(1)、已知a^m=1，aⁿ=2，求a^5m+2n的值；

(2)、已知x³=m，x⁵=n，试用含m、n的代数式表示x¹⁴

(3)、如果等式（2a-1）^a+2=1，求a的值.

查看试题解析

四、解答题

22. 若xⁿ=2，yⁿ=3，求（x²y）²ⁿ的值

查看试题解析
23.

(1)、已知m＋4n-3=0，求2^m·16ⁿ的值．

(2)、已知n为正整数，且x²ⁿ＝4，求（x³ⁿ）²－2（x²）²ⁿ的值．

查看试题解析
24. 阅读理解：我们知道一般地，加减运算是互逆运算，乘除运算也是互逆运算；其实乘方运算也有逆运算；如我们规定式子2³＝8可以变形为log₂8＝3， log₅25＝2也可以变形为5²＝25.在式子2³＝8中， 3叫做以2为底8的对数，记为log₂ 8.一般地，若aⁿ＝b(a＞0且a≠1，b＞0)，则 $n$ 叫做以a为底b的对数，记为log_ab ，即 log_ab＝n.根据上面的规定，请解决下列问题：

(1)、计算：log₃ 1＝， log₂ 32= ， log₂16+ log₂4 ＝，

(2)、小明在计算log₁₀25+log₁₀4 的时候，采用了以下方法：
设log₁₀25=x， log₁₀4=y

∴ 10^x=25 10^y=4

∴ 10^x+y=10^x×10^y=25×4=100=10²

∴ x+y=2

∴ log₁₀25+log₁₀4=2通过以上计算，我们猜想log_aM+ log_aN等于多少，请证明你的猜想.

查看试题解析
25.
理解：我们知道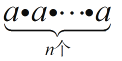： =aⁿ ， a^{m $\cdot$}aⁿ=a^m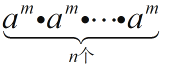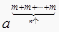⁺ⁿ ，（a^m）ⁿ= = =a^mn ，上述式子反之亦成立，请解决下列问题．

(1)、若x^m⁺²•x^m⁺³=x⁹成立，求m的值；

(2)、若2^x=3，2^y=5，求2^3x+2y+2的值；

(3)、若2^x×4^2x×8^3x=2²⁸ ，求x的值；

(4)、比较2³⁰⁰与3²⁰⁰的大小．

查看试题解析