云南省文山壮族苗族自治州广南县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-20 类型:期末考试
一、单选题
-
1. △ABC中,∠A=60°,∠B=80°,则∠C的度数为( )A、80° B、40° C、60° D、50°2. 下列各图中,不能表示y是x的函数的是( )A、
 B、
B、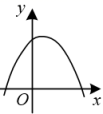 C、
C、 D、
D、 3. 下列各式中,最简二次根式是( )A、 B、 C、 D、4. 若以下列各组数值作为三角形的三边长,则不能围成直角三角形的是( )A、4、6、8 B、3、4、5 C、5、12、13 D、1、3、5. 如图,直线AB∥CD,直线AB、CD被直线EF所截,交点分别为点M、点N,若∠AME=130°,则∠DNM的度数为( )
3. 下列各式中,最简二次根式是( )A、 B、 C、 D、4. 若以下列各组数值作为三角形的三边长,则不能围成直角三角形的是( )A、4、6、8 B、3、4、5 C、5、12、13 D、1、3、5. 如图,直线AB∥CD,直线AB、CD被直线EF所截,交点分别为点M、点N,若∠AME=130°,则∠DNM的度数为( ) A、30° B、40° C、50° D、60°6. 下列命题中,真命题是( )A、若一个三角形的三边长分别是a、b、c,则有 B、(6,0)是第一象限内的点 C、所有的无限小数都是无理数 D、正比例函数()的图象是一条经过原点(0,0)的直线7. 在一次爱心捐助活动中,八年级(1)班40名同学共捐款275元,已知同学们捐款的面额只有5元、10元两种,求捐5元和10元的同学各有多少名?若设捐5元的同学有x名,捐10元的有y名,则可列方程组为( )A、 B、 C、 D、8. 如图,直线l是一次函数的图象,下列说法中,错误的是( )
A、30° B、40° C、50° D、60°6. 下列命题中,真命题是( )A、若一个三角形的三边长分别是a、b、c,则有 B、(6,0)是第一象限内的点 C、所有的无限小数都是无理数 D、正比例函数()的图象是一条经过原点(0,0)的直线7. 在一次爱心捐助活动中,八年级(1)班40名同学共捐款275元,已知同学们捐款的面额只有5元、10元两种,求捐5元和10元的同学各有多少名?若设捐5元的同学有x名,捐10元的有y名,则可列方程组为( )A、 B、 C、 D、8. 如图,直线l是一次函数的图象,下列说法中,错误的是( ) A、 , B、若点(-1,)和点(2,)是直线l上的点,则 C、若点(2,0)在直线l上,则关于x的方程的解为 D、将直线l向下平移b个单位长度后,所得直线的解析式为
A、 , B、若点(-1,)和点(2,)是直线l上的点,则 C、若点(2,0)在直线l上,则关于x的方程的解为 D、将直线l向下平移b个单位长度后,所得直线的解析式为二、填空题
-
9. 5的算术平方根是.10. 甲、乙两名篮球运动员进行每组10次的投篮训练,5组投篮结束后,两人的平均命中数都是7次,方差分别是 , , 则在本次训练中,运动员的成绩更稳定.11. 如图,在△ABC中,点D为BC边延长线上一点,若∠ACD=75°,∠A=45°,则∠B的度数为 .
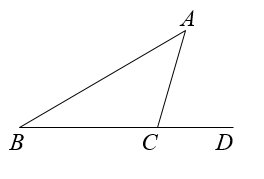 12. 若点(-1,m)与点(n,2)关于y轴对称,则的值为 .13. 已知x、y满足方程组 , 则的值为 .14. △ABC中,AB= , AC=10,BC边上的高AD=6,则BC边长为 .
12. 若点(-1,m)与点(n,2)关于y轴对称,则的值为 .13. 已知x、y满足方程组 , 则的值为 .14. △ABC中,AB= , AC=10,BC边上的高AD=6,则BC边长为 .三、解答题
-
15. 计算:16. 如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
 17. 已知x,y满足 , 求x、y的值.18. 如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.
17. 已知x,y满足 , 求x、y的值.18. 如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.
 19. 在边长为1个单位长度的小正方形网格中,建立平面直角坐标系,已知点O为坐标原点,点C的坐标为(3,1)
19. 在边长为1个单位长度的小正方形网格中,建立平面直角坐标系,已知点O为坐标原点,点C的坐标为(3,1) (1)、写出点A和点B的坐标,并在图中画出与△ABC关于x轴对称的图形△;(2)、写出点B1的坐标,连接CB1 , 则线段CB1的长为 . (直接写出得数)20. 艺术节前夕,为了增添节日气氛,某校决定采购大小两种型号的气球装扮活动场地,计划购买4盒大气球,x盒小气球().A、B两个商场中,两种型号的气球原价一样,都是大气球50元/盒,小气球10元/盒,但给出了不同的优惠方案:
(1)、写出点A和点B的坐标,并在图中画出与△ABC关于x轴对称的图形△;(2)、写出点B1的坐标,连接CB1 , 则线段CB1的长为 . (直接写出得数)20. 艺术节前夕,为了增添节日气氛,某校决定采购大小两种型号的气球装扮活动场地,计划购买4盒大气球,x盒小气球().A、B两个商场中,两种型号的气球原价一样,都是大气球50元/盒,小气球10元/盒,但给出了不同的优惠方案:A商场:买一盒大气球,送一盒小气球;
B商场:一律九折优惠;
(1)、分别写出在两个商场购买时需要的花费y(元)与x(盒)之间的关系式;(2)、如果学校最终决定购买10盒小气球,那么选择在哪个商场购买比较合算?21. 如图,已知点A、点B在数轴上表示的数分别是-20、64,动点M从点A出发,以每秒若干个单位长度的速度向右匀速运动,动点N从点B出发,以每秒若干个单位长度的速度向左匀速运动.若点M、N同时出发,则出发后12秒相遇;若点N先出发7秒,则点M出发10秒后与点N相遇.动点M、N运动的速度分别是多少? 22. 为了解八年级学生的数学知识技能水平,教育局组织了一次数学知识竞赛,满分为100分.为掌握甲、乙两校学生本次竞赛的情况,李老师分别从两个学校的成绩中都随机抽取20个进行整理和分析.李老师将抽取的成绩用x表示,分为A、B、C、D、E五个等级(A:;B:;C:;D:;E:),已知部分信息如下:
22. 为了解八年级学生的数学知识技能水平,教育局组织了一次数学知识竞赛,满分为100分.为掌握甲、乙两校学生本次竞赛的情况,李老师分别从两个学校的成绩中都随机抽取20个进行整理和分析.李老师将抽取的成绩用x表示,分为A、B、C、D、E五个等级(A:;B:;C:;D:;E:),已知部分信息如下:甲校抽取的20名同学的成绩(单位:分)为:91,83,92,80,79,82,82,77,82,80,75,63,56,85,91,70,82,76,64,82
已知乙校抽取的成绩中,有1名同学的成绩不超过60分.
乙校抽取的学生成绩扇形统计图
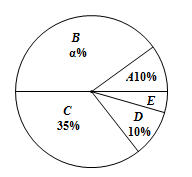
甲、乙两校抽取的学生成绩数据统计表
班级
甲校
乙校
平均数
78.6
78.4
中位数
b
80
众数
c
80
根据以上信息,解答下列问题:
(1)、直接写出上述图表中a、b、c的值: , , ;(2)、不用计算,根据统计表,判断哪个学校的成绩好一些?并说明理由;(3)、若甲、乙两校的八年级学生人数分别为420人、450人,且都参加了此次知识竞赛,估计本次竞赛中,两个学校共有多少人的成绩达到A级?23. 如图,一次函数的图象与x轴、y轴分别交于点A、B(0,6),与正比例函数的图象交于点C(1,m). (1)、求一次函数的解析式;(2)、比较和的大小;(3)、点N为正比例函数图象上的点(不与C重合),过点N作NE⊥x轴于点E(n,0),交直线于点D,当=AB时,求点N的坐标.
(1)、求一次函数的解析式;(2)、比较和的大小;(3)、点N为正比例函数图象上的点(不与C重合),过点N作NE⊥x轴于点E(n,0),交直线于点D,当=AB时,求点N的坐标.