云南省昆明市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-20 类型:期末考试
一、单选题
-
1. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,11 C、1,3,5 D、5,6,102. 下列图形对称轴条数最多的是( )A、等边三角形 B、长方形 C、等腰三角形 D、线段3. 如果把分式中的和都扩大2倍,那么分式的值( )A、扩大2倍 B、不变 C、缩小2倍 D、缩小4倍4. 已知,x2+kx+9是一个完全平方式,则k的值是( )A、-6 B、3 C、6 D、±65. 如图,点、、、在同一条直线上,已知 , , 添加下列条件中的一个:①;②;③;④ . 其中不能确定的是( )
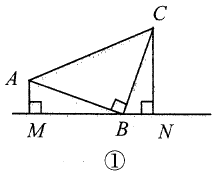
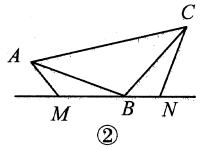
 A、① B、② C、③ D、④6. 如图, , , , 则下列结论:①;②;③;④ . 成立的是( )
A、① B、② C、③ D、④6. 如图, , , , 则下列结论:①;②;③;④ . 成立的是( ) A、①②③ B、①②④ C、②③④ D、①②③④7. 如图,在中,是的垂直平分线,的周长为 , 的周长为 , 则的长为( )
A、①②③ B、①②④ C、②③④ D、①②③④7. 如图,在中,是的垂直平分线,的周长为 , 的周长为 , 则的长为( ) A、 B、 C、 D、8. 若 , , , 则的值为( )A、 B、 C、1 D、
A、 B、 C、 D、8. 若 , , , 则的值为( )A、 B、 C、1 D、二、填空题
-
9. 计算 .10. 分解因式 .11. 若分式有意义,则的取值范围是 .12. 如图,一把直尺的一边缘经过直角三角形的直角顶点 , 交斜边于点;直尺的另一边缘分别交、于点、 , 若 , , 则度.
 13. 如图,三角形纸片中, , , . 沿过点的直线折叠这个三角形,使点落在边上的处,折痕为 , 则周长为 .
13. 如图,三角形纸片中, , , . 沿过点的直线折叠这个三角形,使点落在边上的处,折痕为 , 则周长为 . 14. 利用一边为另一边为的等腰三角形做拼图游戏,按照如图所示的方式组合,当使用第个等腰三角形时,所拼成的图形的周长为 .
14. 利用一边为另一边为的等腰三角形做拼图游戏,按照如图所示的方式组合,当使用第个等腰三角形时,所拼成的图形的周长为 .
三、解答题
-
15. 计算下列各题)(1)、(2)、16. 分解因式(1)、(2)、17. 如图,在平面直角坐标系中,三个顶点的坐标为、、 .
 (1)、在图中作出关于轴的对称图形;(2)、请直接写出点的坐标;(3)、在轴上画出一点使的值最小.18. 如图,在中,、分别是上的高和中线, , , 求的长.
(1)、在图中作出关于轴的对称图形;(2)、请直接写出点的坐标;(3)、在轴上画出一点使的值最小.18. 如图,在中,、分别是上的高和中线, , , 求的长. 19. 先化简,再求值: , 其中 .20. 解分式方程 .
19. 先化简,再求值: , 其中 .20. 解分式方程 .