山东省滨州市阳信县2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-01-20 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $∠ B A C$ 的平分线，点 $E$ 、 $F$ 分别是 $A D$ 的三等分点，若 $△ A B C$ 的面积为 $12 c m^{2}$ ，则图中阴影部分的面积为（）

A、 $4 c m^{2}$ B、 $4.5 c m^{2}$ C、 $5 c m^{2}$ D、 $6 c m^{2}$

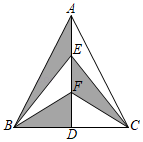查看试题解析
2. 下面运算结果为 $a^{6}$ 的是 $($ $)$

A、 $a^{3} + a^{3}$ B、 $a^{8} \div a^{2}$ C、 $a^{2} • a^{3}$ D、 ${(- a^{2})}^{3}$

查看试题解析
3. 如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）

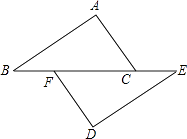A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC

查看试题解析
4. 下列式子：① $\frac{2}{x}$ ，② $\frac{x}{2}$ ，③ $\frac{3}{2 x^{2} - 1}$ ，④ $\frac{x}{x - y}$ ，其中是分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若直角三角形的三边长为6，8，m，则m²的值为（）

A、10 B、100 C、28 D、100或28

查看试题解析
6. 下列因式分解正确的是（）

A、 $a^{2} + 4 a + 4 = (a + 2)^{2}$ B、 $- 4 a + a^{2} = - a (4 + a)$ C、 $(a - 3)^{2} = a^{2} - 6 a + 9$ D、 $a^{2} - 2 a + 1 = a (a - 2) + 1$

查看试题解析
7. 如图，BP平分∠ABC，D为BP上一点，E，F分别在BA，BC上，且满足DE＝DF，若∠BED＝140°，则∠BFD的度数是（）

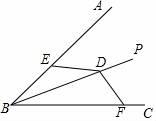A、40° B、50° C、60° D、70°

查看试题解析
8. 与 $\sqrt{5}$ 可以合并的二次根式是（）

A、 $\sqrt{10}$ B、 $\sqrt{15}$ C、 $\sqrt{20}$ D、 $\sqrt{25}$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 8$ ， $D$ 是线段 $B C$ 上的动点（不含端点 $B$ 、 $C$ ）．若线段 $A D$ 长为正整数，则点 $D$ 的个数共有（）

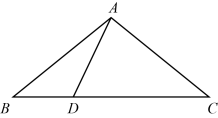A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 如图，在长方形 $A B C D$ 中无重叠放入面积分别为 $16 c m^{2}$ 和 $12 c m^{2}$ 的两张正方形纸片，则图中空白部分的面积为（） $c m^{2}$

A、 $16 - 8 \sqrt{3}$ B、 $- 12 + 8 \sqrt{3}$ C、 $8 - 4 \sqrt{3}$ D、 $4 - 2 \sqrt{3}$

查看试题解析
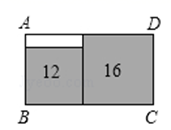11. 若关于x的分式方程 $\frac{x - m}{x} = m - 1$ 无解，则m的值为（）

A、0 B、2 C、0或2 D、±2

查看试题解析
12. 2020年初，湖北武汉出现了“新型冠状病毒感染肺炎”疫情，面对突如其来的疫情，全国人民众志成城，携手抗疫．甲、乙两单位为“新冠疫情”分别捐款4800元、6000元，已知甲单位捐款人数比乙单位少50人，而甲单位人均捐款数比乙单位多1元，若设甲单位有x人捐款，则所列方程是（）

A、 $\frac{4800}{x} = \frac{6000}{x + 50} + 1$ B、 $\frac{4800}{x} = \frac{6000}{x - 50} + 1$ C、 $\frac{4800}{x} = \frac{6000}{x + 50} - 1$ D、 $\frac{4800}{x} = \frac{6000}{x - 50} - 1$

查看试题解析

二、填空题

13. 因式分解： $8 a^{3} - 2 a b^{2} =$ ．

查看试题解析
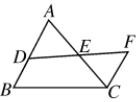
14. 若 $x = 4$ 是分式方程 $\frac{a - 2}{x} = \frac{1}{x - 3}$ 的根，则a的值为．

查看试题解析
15. 如图，点D在AB 上，AC，DF 交于点 E，AB∥FC，DE=EF，AB=15，CF=8，则BD=.

查看试题解析
16. 已知分式 $\frac{x + 1}{2 - x}$ ，当x取a时，该分式的值为0；当x取b时，分式无意义，则a^b的值等于．

查看试题解析
17. 已知 $x=y+4$ ，则代数式 $x^{2} - {2xy+y}^{2} - 25$ 的值为．

查看试题解析
18. 已知点A（x ， ﹣4）与点B（3，y）关于x轴对称，那么x+y的值为．

查看试题解析
19. 若规定符号“*”的意义是 $a * b = a b - b^{2}$ ，则 $2 * (\sqrt{2} - 1)$ 的值是．

查看试题解析
20. 如果正整数a、b、c满足等式a²+b²＝c² ，那么正整数a、b、c叫做勾股数，某同学将自探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为．

查看试题解析

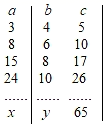
三、解答题

21. 计算与化简求值：

(1)、计算： $\sqrt{6} \div \sqrt{\frac{1}{3}} - | 4 - 3 \sqrt{2} | + (\sqrt{5} - 1)^{0}$ ；

(2)、先化简，再求值（x﹣1）（x﹣2）﹣（x+1）² ，其中 $x = \frac{1}{2}$ ．

(3)、已知 $(x + a) (x - \frac{3}{2})$ 的结果中不含关于字母x的一次项，求（a+2）²﹣（1﹣a）（﹣a﹣1）的值．

(4)、先化简代数式 $\frac{a^{2} - 2 a + 1}{a^{2} - 4} \div (1 - \frac{3}{a + 2})$ ，再从2，﹣2，1，﹣1四个数中选择一个你喜欢的数代入求值．

查看试题解析
22. 解分式方程：

(1)、解方程： $\frac{x}{x - 1} - 1 = \frac{2}{x^{2} - 1}$ ．

(2)、若关于x的分式方程 $\frac{3 - m x}{x - 2} = 5$ 与 $\frac{2 x + 1}{x - 1} = 3$ 的解相同，求m的值．

查看试题解析
23. 先阅读后解题．
已知m²+2m+n²﹣6n+10＝0，求m和n的值．
解：把等式的左边分解因式：（m²+2m+1）+（n²﹣6n+9）＝0．
即（m+1）²+（n﹣3）²＝0．
因为（m+1）²≥0，（n﹣3）²≥0．
所以m+1＝0，n﹣3＝0即m＝﹣1，n＝﹣3．
利用以上解法，解下列问题：

(1)、已知：x²﹣4x+y²+2y+5＝0，求x和y的值．

(2)、已知a，b，c是△ABC的三边长，满足a²+b²＝12a+8b﹣52且△ABC为等腰三角形，求c．

查看试题解析
24. 如图，在等腰Rt△ABC中，∠ACB＝90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF.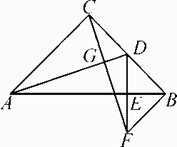

(1)、求证：AD⊥CF；

(2)、连接AF，试判断△ACF的形状，并说明理由．

查看试题解析
25. 中国是最早发现并利用茶的国家，形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开．某茶店用4000元购进了A种茶叶若干盒，用8400元购进B种茶叶若干盒，所购B种茶叶比A种茶叶多10盒，且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍．

(1)、A ， B两种茶叶每盒进价分别为多少元？

(2)、第一次所购茶叶全部售完后第二次购进A ， B两种茶叶共100盒（进价不变），A种茶叶的售价是每盒300元，B种茶叶的售价是每盒400元．两种茶叶各售出一半后，为庆祝国际茶日，两种茶叶均打七折销售，全部售出后，第二次所购茶叶的利润为5800元（不考虑其他因素），求本次购进A ， B两种茶叶各多少盒？

查看试题解析
26. 如图所示，已知 $Δ A B C$ 中， $∠ B = 90 °$ ， $A B = 16 c m$ ， $A C = 20 c m$ ， $P$ 、 $Q$ 是 $Δ A B C$ 的边上的两个动点，其中点 $P$ 从点 $A$ 开始沿 $A \to B$ 方向运动，且速度为每秒 $1 c m$ ，点 $Q$ 从点 $B$ 开始沿 $B \to C \to A$ 方向运动，且速度为每秒 $2 c m$ ，它们同时出发，设出发的时间为 $t s$ ．

(1)、则 $B C =$ $c m$ ；

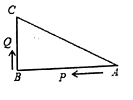(2)、当 $t$ 为何值时，点 $P$ 在边 $A C$ 的垂直平分线上？此时 $C Q =$ ?

(3)、当点 $Q$ 在边 $C A$ 上运动时，直接写出使 $Δ B C Q$ 成为等腰三角形的运动时间．

查看试题解析