辽宁省铁岭市铁岭县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-20 类型:期末考试
一、单选题
-
1. 有一个三角形的两边长分别为2和5,则第三边的长可能是( )A、2 B、2.5 C、3 D、52. 下列交通指示标识中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )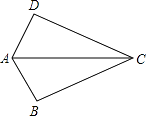 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°5. 若 , , 则的值为( )A、5 B、2 C、10 D、无法计算6. 如图, , , , , 垂足分别为、 , 且 , , 则的长是( )
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°5. 若 , , 则的值为( )A、5 B、2 C、10 D、无法计算6. 如图, , , , , 垂足分别为、 , 且 , , 则的长是( ) A、2 B、3 C、5 D、77. 如图,在中, , , 则的外角的度数是( )
A、2 B、3 C、5 D、77. 如图,在中, , , 则的外角的度数是( ) A、 B、 C、 D、8. 如图,是等边中边上的点, , , 则是( )
A、 B、 C、 D、8. 如图,是等边中边上的点, , , 则是( )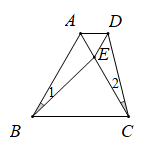 A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定9. 关于的分式方程的解为正数,则的取值范围是( )A、 B、 C、且 D、且10. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )
A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定9. 关于的分式方程的解为正数,则的取值范围是( )A、 B、 C、且 D、且10. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )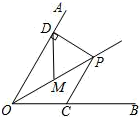 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为 .12. 当时,分式的值为0.13. 因式分解: .14. 如图 , , 若 , 则 .
 15. 若 , , 则 .16. 一个多边形,每个外角都是 , 则这个多边形是边形.17. 如图,∠ , 是 , 垂直平分线的交点,则的度数是 .
15. 若 , , 则 .16. 一个多边形,每个外角都是 , 则这个多边形是边形.17. 如图,∠ , 是 , 垂直平分线的交点,则的度数是 . 18. 如图,在中, , 点在边上,且 , 过上一点作 , 交、的延长线、的延长线分别于点 , 和 , 有下列结论:①图中共有4个等腰三角形;②;③;④ . 其中正确的结论有(请填写序号).
18. 如图,在中, , 点在边上,且 , 过上一点作 , 交、的延长线、的延长线分别于点 , 和 , 有下列结论:①图中共有4个等腰三角形;②;③;④ . 其中正确的结论有(请填写序号).
三、解答题
-
19. 完成下列各题:(1)、计算:①
②
(2)、因式分解:①②
20. 解下列分式方程:(1)、(2)、21. 如图,平面直角坐标系中,每个小正方形的边长都是1. (1)、请画出关于轴对称的轴对称图形;并写出点 , , 三点的坐标;(2)、在轴、轴上找到与点、距离相等的点 , .
(1)、请画出关于轴对称的轴对称图形;并写出点 , , 三点的坐标;(2)、在轴、轴上找到与点、距离相等的点 , .(要求:尺规作图,不写画法,保留作图痕迹).
22. 先化简 ,再从 , ,0,1,2中选一个合适的数作为x的值代入求值.23. 如图 , , 垂足分别为点 , , 且 , , 点 , , , 在同一条直线上, , 相交于点 .
求证:
(1)、;(2)、 .24. 某商场11月初花费15 000元购进一批某品牌英语点读笔,因深受顾客喜爱,销售一空.该商场于12月初又花费24 000元购进一批同品牌英语点读笔,且所购数量是11月初的1.5倍,但每支进价涨了10元.(1)、求商场11月初购进英语点读笔多少支?(2)、11月份商场该品牌点读笔每支的售价是270元,若12月份购买的点读笔全部售完,且所获利润是11月份利润的1.2倍,求12月份该品牌点读笔每支的售价?25. 如图:在中, , , 点为的中点,点为直线上的动点(不与点 , 重合),连接 , , 以为边在的上方作等边 , 连接 . (1)、是三角形;(2)、如图1,当点在边上时,运用(1)中的结论证明;(3)、如图2,当点在的延长线上时,(2)中的结论是否依然成立?若成立,请加以证明,若不成立,请说明理由.
(1)、是三角形;(2)、如图1,当点在边上时,运用(1)中的结论证明;(3)、如图2,当点在的延长线上时,(2)中的结论是否依然成立?若成立,请加以证明,若不成立,请说明理由.