辽宁省抚顺市望花区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-20 类型:期末考试
一、单选题
-
1. 下列说法正确的是( )A、全等三角形是指形状相同的两个三角形 B、全等三角形的周长和面积分别相等 C、所有的直角三角形都是全等三角形 D、所有的等边三角形都是全等三角形2. 冠状病毒是一大类病毒的总称,在电子显微镜下可以观察到他们的表面有类似日冕状突起,看起来像王冠一样因此被命名为冠状病毒,其平均直径大约0.0000001米,将0.0000001用科学记数法表示为 ( )A、 B、 C、 D、3. 下列运算正确的是( )A、(a2)3=a6 B、a2•a3=a6 C、a7÷a=a7 D、(﹣2a2)3=8a64. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )A、a=5,b=﹣6 B、a=5,b=6 C、a=1,b=6 D、a=1,b=﹣66. 用直角三角板作△ABC的高,下列作法正确的是( )A、
5. 若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )A、a=5,b=﹣6 B、a=5,b=6 C、a=1,b=6 D、a=1,b=﹣66. 用直角三角板作△ABC的高,下列作法正确的是( )A、 B、
B、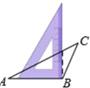 C、
C、 D、
D、 7. 如图,在△ABC中,AB=AC,点D是BC的中点,那么图中的全等三角形的对数是( )
7. 如图,在△ABC中,AB=AC,点D是BC的中点,那么图中的全等三角形的对数是( ) A、0 B、1 C、2 D、38. 如图,△ABC中BD、CD平分∠ABC、∠ACB过D作直线平行于BC,交AB、AC于E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系是( )
A、0 B、1 C、2 D、38. 如图,△ABC中BD、CD平分∠ABC、∠ACB过D作直线平行于BC,交AB、AC于E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系是( )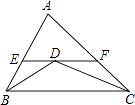 A、EF=BE+CF B、EF>BE+CF C、EF<BE+CF D、不能确定9. 随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产30万件产品,现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同,设更新技术前每天生产x万件,依据题意得( )A、 B、 C、 D、
A、EF=BE+CF B、EF>BE+CF C、EF<BE+CF D、不能确定9. 随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产30万件产品,现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同,设更新技术前每天生产x万件,依据题意得( )A、 B、 C、 D、二、多选题
-
10. 如图,为估计池塘岸边A,B两点间的距离,小方在池塘的一侧选取一点O,测得米,米,A,B间的距离可能是( )
 A、12米 B、10米 C、15米 D、8米
A、12米 B、10米 C、15米 D、8米三、填空题
-
11. (﹣2)0+3﹣2= .12. 若分式 有意义,则x的取值范围是.13. 如图是中国古代建筑中的一个正六边形的窗户,则它的内角和为 .
 14. 如图,学校大门口的电动伸缩门,其中间部分都是四边形的结构,这是应用了四边形的 .
14. 如图,学校大门口的电动伸缩门,其中间部分都是四边形的结构,这是应用了四边形的 . 15. 如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为.
15. 如图,△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为. 16. 边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为.
16. 边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为. 17. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm.
17. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm.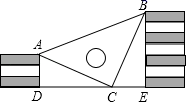 18. 如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=50°,连接AC、BD交于点M,连接OM.下列结论:①AC=BD,②∠AMB=50°;③OM平分∠AOD;④MO平分∠AMD.其中正确的结论是 . (填序号)
18. 如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=50°,连接AC、BD交于点M,连接OM.下列结论:①AC=BD,②∠AMB=50°;③OM平分∠AOD;④MO平分∠AMD.其中正确的结论是 . (填序号)
四、解答题
-
19.(1)、计算:x(x2y2﹣xy)÷x2y;(2)、分解因式:3bx2+6bxy+3by2 .20.(1)、计算:(1);(2)、解方程:1.21. 如图,已知△ABC的三个顶点的坐标分别为A(﹣3,2),B(﹣6,﹣4),C(﹣2,﹣1).
 (1)、画出△ABC关于y轴成轴对称的△DEF,点A的对应点为点D,写出点D的坐标;(2)、请直接写出△DEF的面积;(3)、在y轴上画出点P,使PA+PB最小,并写出点P的坐标.22. 为庆祝中国共产党的百年华诞,某校要进行美化校园,各班同学设计热爱祖国的板报.八年一班学生在设计板报时,在黑板中间画一个半径为R的大圆,然后挖去半径为r的四个小圆,分别作为热爱中国共产党、热爱人民、认同中华文化和继承革命传统四个学习区域.请计算当R=7.8cm,r=1.1cm时剩余部分的面积.(结果保留π)
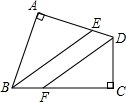
(1)、画出△ABC关于y轴成轴对称的△DEF,点A的对应点为点D,写出点D的坐标;(2)、请直接写出△DEF的面积;(3)、在y轴上画出点P,使PA+PB最小,并写出点P的坐标.22. 为庆祝中国共产党的百年华诞,某校要进行美化校园,各班同学设计热爱祖国的板报.八年一班学生在设计板报时,在黑板中间画一个半径为R的大圆,然后挖去半径为r的四个小圆,分别作为热爱中国共产党、热爱人民、认同中华文化和继承革命传统四个学习区域.请计算当R=7.8cm,r=1.1cm时剩余部分的面积.(结果保留π) 23. 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.
23. 如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.求证:BE∥DF.
 24. 新冠肺炎疫情发生后,全社会积极参与疫情防控工作,由于疫情形势严峻,口罩的需求量增大.某医疗器械生产厂家接到A型口罩40万只和B型口罩45万只的订单.该工厂有甲、乙两个车间,甲车间生产A型口罩,乙车间生产B型口罩.已知乙车间每天生产的口罩数比甲车间每天生产的口罩数量多50%,结果乙车间比甲车间提前2天完成订单任务,求甲车间每天生产A型口罩多少万只?25. 某游乐场部分平面图如图所示,点C、E、A在同一直线上,点D、E、B在同一直线上,DB⊥AB.测得A处与E处的距离为80m,C处与E处的距离为40m,∠C=90°,∠BAE=30°.
24. 新冠肺炎疫情发生后,全社会积极参与疫情防控工作,由于疫情形势严峻,口罩的需求量增大.某医疗器械生产厂家接到A型口罩40万只和B型口罩45万只的订单.该工厂有甲、乙两个车间,甲车间生产A型口罩,乙车间生产B型口罩.已知乙车间每天生产的口罩数比甲车间每天生产的口罩数量多50%,结果乙车间比甲车间提前2天完成订单任务,求甲车间每天生产A型口罩多少万只?25. 某游乐场部分平面图如图所示,点C、E、A在同一直线上,点D、E、B在同一直线上,DB⊥AB.测得A处与E处的距离为80m,C处与E处的距离为40m,∠C=90°,∠BAE=30°.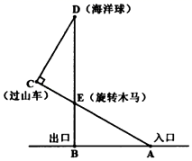 (1)、请求出旋转木马E处到出口B处的距离;(2)、请求出海洋球D处到出口B处的距离;(3)、判断入口A到出口B处的距离与海洋球D到过山车C处的距离是否相等?若相等,请证明;若不相等,请说明理由.26. 已知,点P、点Q分别是等边△ABC的边AB、BC所在直线上的动点(端点除外).点P、点Q以相同的速度,同时从点A、点B出发,连接AQ、CP,直线AQ、CP相交于点M.
(1)、请求出旋转木马E处到出口B处的距离;(2)、请求出海洋球D处到出口B处的距离;(3)、判断入口A到出口B处的距离与海洋球D到过山车C处的距离是否相等?若相等,请证明;若不相等,请说明理由.26. 已知,点P、点Q分别是等边△ABC的边AB、BC所在直线上的动点(端点除外).点P、点Q以相同的速度,同时从点A、点B出发,连接AQ、CP,直线AQ、CP相交于点M. (1)、如图1,当点P、Q分别在AB、BC边上时,
(1)、如图1,当点P、Q分别在AB、BC边上时,①求证:△ABQ≌△CAP;
②当点P、点Q分别在AB、BC边上运动时,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
(2)、如图2,当点P、Q分别在AB、BC的延长线上运动时,请直接写出∠QMC的度数.
-