吉林省延边朝鲜族自治州2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-20 类型：期末考试

进入出卷网下载

一、单选题

1. 三个数 $2^{0}$ ， $3^{- 2}$ ， ${(- 3)}^{- 1}$ 中，负数的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 下列图案中，不是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
3. 下列计算中，正确的是（）

A、 ${(a + 2 b)}^{2} = a + 4 b^{2}$ B、 $a \cdot a^{4} = a^{4}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(^{} b)}^{2} = a^{6} b^{2}$

查看试题解析
4. 化简 $\frac{x}{2} \div \frac{x - y}{2 x} - \frac{y^{2}}{x - y}$ ，正确结果是（）

A、 $\frac{1 - y^{2}}{x - y}$ B、 $x - y$ C、 $x + y$ D、 $2 x - 2 y$

查看试题解析
5. 如图，在 $△ A B C$ 中，AD是角平分线，且 $A D = A C$ ，若 $∠ B A C = 60 °$ ，则 $∠ B$ 的度数是（）

A、45° B、50° C、52° D、58°

查看试题解析
6. 八年级学生去距学校10km的博物馆参观，一部分学生骑自行车先走，过了15min后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是自行车速度的2倍，设汽车到博物馆所需的时间为xh，则下列方程正确的是（）

A、 $\frac{10}{x + 0.25} = 2 \times \frac{10}{x}$ B、 $\frac{10}{x - 0.25} = 2 \times \frac{10}{x}$ C、 $\frac{10}{x} = 2 \times \frac{10}{x + 0.25}$ D、 $\frac{10}{x} = 2 \times \frac{10}{x - 0.25}$

查看试题解析

二、填空题

7. 计算： $2 a^{2} \cdot 5 a =$ ．

查看试题解析
8. 若 $0.000015 = 1.5 \times 1 0^{n}$ ，则 $n =$ ．

查看试题解析
9. 分式方程 $\frac{1}{x + 1} = \frac{2}{3 x}$ 的解是．

查看试题解析
10. 在平面直角坐标系中，点A（m，−5）和点B（−2，n）关于x轴对称，则m+n= ．

查看试题解析
11. 若正多边形的一个外角是45°，则该正多边形的边数是．

查看试题解析
12. 如图， $△ A B C$ 是等腰直角三角形，AB是斜边，以BC为一边在右侧作等边三角形BCD，连接AD与BC交于点E，则 $∠ B E D$ 的度数为度．

查看试题解析
13. 如图，正三角形ABC中，D是AB的中点， $D E ⊥ A C$ 于点E，过点E作 $E F ∥ A B$ 与BC交于点F．若 $B C = 8$ ，则 $△ E F C$ 的周长为．

查看试题解析
14. 如图， $△ A B C$ 中，边AC的垂直平分线与边BC交于点D．将 $△ A D C$ 沿AD折叠后，使点C与点E重合，且 $D E ⊥ A B$ ，若 $∠ B = 50 °$ ，则 $∠ B A E =$ 度．

查看试题解析

三、解答题

15. 计算： $(a - 2) (a + 4) + 2 a (a - 1)$ ．

查看试题解析
16. 化简： $\frac{2}{x^{2} + 2 x} - \frac{1}{x}$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中，点D、E分别在边AB、AC上，BE与CD交于点F， $∠ A = 62 °$ ， $∠ A C D = 25 °$ ， $∠ E F C = 53 °$ ．求 $∠ B D C$ 和 $∠ D B E$ 的度数．

查看试题解析
18. 如图，点A，B，C，D在一条直线上， $A B = C D$ ， $A E ∥ C F$ ， $∠ E = ∠ F$ ．求证： $B E = D F$ ．

查看试题解析
19. 先化简，再求值： ${(x + 2 y)}^{2} - 4 y (x + \frac{1}{2} y)$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$ ．

查看试题解析
20. 如图在 $5 \times 5$ 的正方形网格中，每个小正方形的顶点称为格点．点A，点B都在格点上，按下列要求画图．

(1)、在图①中，AB为一边画 $△ A B C$ ，使点C在格点上，且 $△ A B C$ 是轴对称图形；

(2)、在图②中，AB为一腰画等腰三角形，使点C在格点上；

(3)、在图③中，AB为底边画等腰三角形，使点C在格点上．

查看试题解析
21. 如图，灯塔B在灯塔A的正东方向，且 $A B = 75 k m$ ．灯塔C在灯塔A的北偏东20°方向，灯塔C在灯塔B的北偏西50°方向．

(1)、求 $∠ A C B$ 的度数；

(2)、一轮船从B地出发向北偏西50°方向匀速行驶，5h后到达C地，求轮船的速度．

查看试题解析
22. 张明3小时清点完一批图书的一半，李强加入清点另一半图书的工作，两人合作1.2小时清点完另一半图书。如果李强单独清点这批图书需要几小时？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD是角平分线，E是AB边上一点，连接ED，CB是 $∠ A C F$ 的平分线，ED的延长线与CF交于点F．

(1)、求证： $B E = C F$ ；

(2)、若 $∠ C D F = 46 °$ ， $A D = D F$ ，则 $∠ A C F =$ 度．

查看试题解析
24.

(1)、数学课堂上老师留了道数学题，如图1，用式子表示空白部分的面积．
甲，乙，丙，丁4名同学表示的式子是：
甲： $10 \times 6 - 10 x - 6 x$
乙： $10 \times 6 - 10 x - 6 x - x^{2}$
丙： $10 \times 6 - 10 x - 6 x + x^{2}$
丁： $(10 - x) (6 - x)$
4名同学中正确的学生是；（填“甲”，“乙”，“丙”，“丁”）

(2)、如图2，有一块长为 $(7 a + 3 b)$ 米，宽为 $(6 a - 3 b)$ 米的长方形空地，计划修筑东西、南北走向的两条道路，其余进行绿化，已知两条道路的宽分别为 $2 a$ 米和 $3 a$ 米，求绿地的面积（用含a，b的式子来表示）

查看试题解析
25. 如图1，两个相同的等边三角形一边重合得到四边形ABCD， $A B = 6 c m$ ．点P从点A出发以 $2 c m / s$ 的速度在三角形的边上沿 $A - C - D$ 方向到点D运动，点Q从点C出发以 $1 c m / s$ 速度沿CB到点B运动．点P的运动时间是 $t (s)$ ，两个点同时出发，到终点停止运动．

(1)、当 $t = 2 s$ 时， $△ P Q C$ 的周长为cm；

(2)、当 $△ A B P$ 为直角三角形时， $t =$ s；

(3)、如图2， $△ A Q P$ 为等边三角形时， $△ A B Q$ 与 $△ A C P$ 是否全等？如果全等证明其结论，并求出此时t的值，如果不全等请说明理由．

查看试题解析
26.

(1)、在数学中，完全平方公式是比较熟悉的，例如 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ ．若 $a - b = 3$ ， $a b = 2$ ，则 $a^{2} + b^{2} =$ ；

(2)、如图1，线段AB上有一点C，以AC、CB为直角边在上方分别作等腰直角三角形ACE和CBF，已知， $E F = 2$ ， $△ A C F$ 的面积为6，设 $A C = a$ ， $B C = b$ ，求 $△ A C E$ 与 $△ C B F$ 的面积之和；

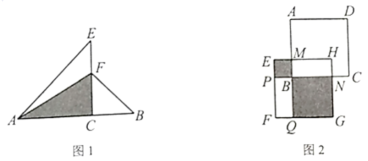(3)、如图2，两个正方形ABCD和EFGH重叠放置，两条边的交点分别为M、N．AB的延长线与FG交于点Q，CB的延长线与EF交于点P，已知 $A M = 7$ ， $C N = 3$ ，阴影部分的两个正方形EPBM和BQGN的面积之和为60，则正方形ABCD和EFGH的重叠部分的长方形BMHN的面积为．

查看试题解析