吉林省四平市伊通满族自治县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-20 类型：期末考试

进入出卷网下载

一、单选题

1. 科学家借助电子显微镜发现新型冠状病毒的平均直径约为0.000000125米，则数据0.000000125用科学记数法表示正确的是（）

A、1.25×10⁸ B、1.25×10^﹣8 C、1.25×10⁷ D、1.25×10^﹣7

查看试题解析
2. 放风筝是我国人民非常喜爱的一项户外娱乐活动，下列风筝剪纸作品中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一个三角形三个内角之比为1：3 ：5，则最小的角的度数为（）

A、20° B、30° C、40° D、60°

查看试题解析
4. 若分式 $\frac{x - 1}{2 x}$ 的值为0，则x的值是（）

A、0 B、1 C、2 D、-1

查看试题解析
5. 如图，点O在AD上，∠A＝∠C，∠AOC＝∠BOD，AB＝CD，AD＝8，OB＝3，则OC的长为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 如图，在△ABC中，DE是AC的垂直平分线，分别交BC，AC于D，E两点，若∠B＝80°，∠C＝35°，则∠BAD的度数为（）

A、65° B、35° C、30° D、25°

查看试题解析

二、填空题

7. 正五边形每个内角的度数是.

查看试题解析
8. 若分式 $\frac{1 + 2 x}{1 - 2 x}$ 有意义，则x的取值范围是．

查看试题解析
9. 已知等腰三角形一个外角的度数为 $108^{\circ}$ ，则顶角度数为.

查看试题解析
10. 在平面直角坐标系中，点A（m，﹣4）与点B（﹣5，n）关于y轴对称，则点（m，n）在第象限．

查看试题解析
11. （﹣2021）⁰＝．

查看试题解析
12. 如图，在△ABC中，∠C＝90°，AD平分∠BAC，点D到AB的距离为7cm，CD＝cm.

查看试题解析
13. 如图，两根旗杆CA，DB相距20米，且CA⊥AB，DB⊥AB，某人从旗杆DB的底部B点沿BA走向旗杆CA底部A点．一段时间后到达点M，此时他分别仰望旗杆的顶点C和D，两次视线的夹角∠CMD＝90°，且CM＝DM．已知旗杆BD的高为12米，该人的运动速度为每秒2米，则这个人从点B到点M所用时间是秒．

查看试题解析
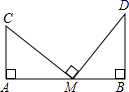14. 斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度．如图，某路口的斑马线路段 $A － B － C$ 横穿双向行驶车道，其中 $A B ＝ B C ＝ 12$ 米，在绿灯亮时，小敏共用 $22$ 秒通过 $A C$ ，其中通过 $B C$ 的速度是通过 $A B$ 速度的 $1.2$ 倍，求小敏通过 $A B$ 时的速度．设小敏通过 $A B$ 时的速度是 $x$ 米/秒，根据题意列方程为．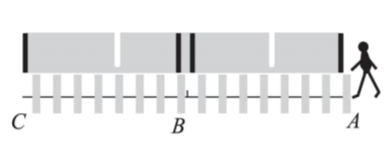

查看试题解析

三、解答题

15. 计算：（2a²•8a²+8a³﹣4a²）÷2a．

查看试题解析
16. 解分式方程： $\frac{2 - x}{x - 3} = 1 + \frac{1}{3 - x}$ ．

查看试题解析
17. 已知：如图，线段BE、DC交于点O，点D在线段AB上，点E在线段AC上，AB＝AC，AD＝AE．求证：∠B＝∠C．

查看试题解析
18. 分解因式：x³y﹣2x²y²+xy³ ．

查看试题解析
19. 有这样一道题：先化简再求值，“ $\frac{x^{2} - 2 x + 1}{x^{2} - 1} \div \frac{x - 1}{x^{2} + x} - x + 1$ ，其中 $x = 2021$ ． ”小华同学把条件“ $x = 2021$ ”错抄成“ $x = 2012$ ”，但他的计算结果也是正确的，请通过计算说明这是怎么回事．

查看试题解析
20. 如图，在△ABC中，AB＝AC，∠A＝36°，AB的垂直平分线交AB于点D，交AC于点E．求证：△BEC是等腰三角形．

查看试题解析
21. 将边长为a的正方形的左上角剪掉一个边长为b的正方形（如图1），将剩下部分按照虚线分割成①和②两部分，将①和②两部分拼成一个长方形（如图2），解答下列问题：

(1)、设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂ ，请用含a，b的式子表示：S₁＝， S₂＝；（不必化简）

(2)、由（1）中的结果可以验证的乘法公式是；

(3)、利用（2）中得到的公式，计算：2021²﹣2020×2022．

查看试题解析
22. 如图，在△ABC中，AB的垂直平分线l₁交AB于点M，交BC于点D，AC的垂直平分线l₂交AC于点N，交BC于点E，l₁与l₂相交于点O，△ADE的周长为10．请你解答下列问题：

(1)、求BC的长；

(2)、试判断点O是否在边BC的垂直平分线上，并说明理由．

查看试题解析
23. 2020年春节寒假期间，小伟同学完成数学寒假作业的情况是这样的：原计划每天都做相同页数的数学作业，做了5天后，由于新冠疫情加重，当地加强了防控措施，对外出进行限制，小伟有更多的时间待在家里，做作业的效率提高到原来的2倍，结果比原计划提前6天完成了数学寒假作业，已知数学寒假作业本共有34页，求小伟原计划每天做多少页数学寒假作业？

查看试题解析
24. 如图，点O是等边△ABC内一点，点D是△ABC外一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，连接OD．

(1)、求证：△OCD是等边三角形；

(2)、当α＝150°时，试判断△AOD的形状，并说明理由；

(3)、当α＝∠AOB，AO＝8cm时，求OC的长度．

查看试题解析