吉林省四平市铁西区2021-2022学年八年级上学期期末考试数学试题
试卷更新日期:2022-01-20 类型:期末考试
一、单选题
-
1. 下列有关绿色、环保主题的四个标志中,是轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 在代数式 中,分式共有( ).A、2个 B、3个 C、4个 D、5个3. 下列不能使用平方差公式因式分解的是( )A、﹣16x2+y2 B、b2﹣a2 C、﹣m2﹣n2 D、4a2﹣49n24. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列错误的等式是( )
2. 在代数式 中,分式共有( ).A、2个 B、3个 C、4个 D、5个3. 下列不能使用平方差公式因式分解的是( )A、﹣16x2+y2 B、b2﹣a2 C、﹣m2﹣n2 D、4a2﹣49n24. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列错误的等式是( ) A、AD=DE B、∠BAE=∠CAD C、BE=DC D、AB=AC5. 如图,在平面直角坐标系中,长方形的顶点的坐标分别为 , 点是的中点,点在上运动,当时,点的坐标是( )
A、AD=DE B、∠BAE=∠CAD C、BE=DC D、AB=AC5. 如图,在平面直角坐标系中,长方形的顶点的坐标分别为 , 点是的中点,点在上运动,当时,点的坐标是( ) A、 B、 C、 D、6. 把分式(均为正)中的的值都扩大为原来的3倍,则分式的值( )A、不变 B、变为原来的3倍 C、变为原来的 D、变为原来的
A、 B、 C、 D、6. 把分式(均为正)中的的值都扩大为原来的3倍,则分式的值( )A、不变 B、变为原来的3倍 C、变为原来的 D、变为原来的二、填空题
-
7. 当时,分式有意义.8. 用科学记数法表示0.00000012为 .9. 一个多边形的内角和是720°,则这个多边形的对角线共有条.10. 多项式 是完全平方式,则m=.
11. 长方形的面积为 , 其中一边长是 , 则另一边长是 .12. 若分式方程有增根,则 .13. 如图,在△ABC中,AC=BC,△ABC的外角∠ACE=100°,则∠A= 度.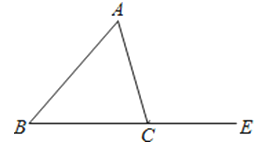 14. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,度.
14. 如图,是等边三角形,是边上的高,是的中点,是上的一个动点,当与的和最小时,度.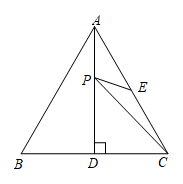
三、解答题
-
15. 利用乘法公式解决下列问题:(1)、若 , , 则;(2)、已知,若满足 , 求值.16. 计算题:17. 因式分解:18. 解分式方程: +1=19. 解方程20. 先化简,再求值: , 其中x =3.21. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
 (1)、画出△ABC关于y轴对称的图形△A1B1C1;(2)、如果点D(a,b)在线段AB上,请直接写出经过(1)的变化后D的对应点D1的坐标;(3)、请计算出的面积.22. 如图,在中, , 于点 , , 平分交于点 , 的延长线交于点 . 求证: .
(1)、画出△ABC关于y轴对称的图形△A1B1C1;(2)、如果点D(a,b)在线段AB上,请直接写出经过(1)的变化后D的对应点D1的坐标;(3)、请计算出的面积.22. 如图,在中, , 于点 , , 平分交于点 , 的延长线交于点 . 求证: . 23. 为了安全与方便,某自助加油站只提供两种自助加油方式:“每次定额只加200元”与“每次定量只加40升”.现有甲、乙两车连续两次同时进入自助加油站加油,甲车选择每次只加40升,乙车选择每次只加200元为比较谁的加油方式更合算,不妨设第一次加油时油价为元/升,第二次加油时油价为元/升,且 . 请回答下列问题:(1)、①甲车两次加油的平均油价为:元/升;
23. 为了安全与方便,某自助加油站只提供两种自助加油方式:“每次定额只加200元”与“每次定量只加40升”.现有甲、乙两车连续两次同时进入自助加油站加油,甲车选择每次只加40升,乙车选择每次只加200元为比较谁的加油方式更合算,不妨设第一次加油时油价为元/升,第二次加油时油价为元/升,且 . 请回答下列问题:(1)、①甲车两次加油的平均油价为:元/升;②乙车两次加油的平均油价为:元/升.
(2)、请比较两车的平均油价,并用数学语言说明哪种加油方式更合算.24. 如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G. (1)、若∠MON=60°,则∠ACG= ;(直接写出答案)(2)、若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)(3)、如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.25. 元旦将至,天猫某电商用4400元购入一批玩具盲盒,然后以每个60元的价格出售,很快售完.电商又以9600元的价格再次购入该商品.数量是第一次购入数量的1.6倍,售价每个上调了16元,进价每个也上调了16元.(1)、该电商第一次购入的玩具盲盒每个进价是多少元?(2)、该电商既要尽快售完第二次购入的玩具盲盒,又要使在这两次销售中获得的总利润不低于4000元.打算将第二次购入的部分盲盒按每个九折出售,最多可将多少个盲盒打折出售?26. 如图1所示,已知点 , 有以点为顶点的直角的两边分别与轴、轴相交于点 .
(1)、若∠MON=60°,则∠ACG= ;(直接写出答案)(2)、若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)(3)、如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.25. 元旦将至,天猫某电商用4400元购入一批玩具盲盒,然后以每个60元的价格出售,很快售完.电商又以9600元的价格再次购入该商品.数量是第一次购入数量的1.6倍,售价每个上调了16元,进价每个也上调了16元.(1)、该电商第一次购入的玩具盲盒每个进价是多少元?(2)、该电商既要尽快售完第二次购入的玩具盲盒,又要使在这两次销售中获得的总利润不低于4000元.打算将第二次购入的部分盲盒按每个九折出售,最多可将多少个盲盒打折出售?26. 如图1所示,已知点 , 有以点为顶点的直角的两边分别与轴、轴相交于点 . (1)、试说明;(2)、若点坐标为 , 点坐标为 , 请直接写出与之间的数量关系;(3)、如图2所示,过点作线段 , 交轴正半轴于点 , 交轴负半轴于点 , 使得点为中点,且 , 绕着顶点旋转直角 , 使得一边交轴正半轴于点 , 另一边交轴正半轴于点 , 此时,和是否还相等,请说明理由;(4)、在(3)条件下,请直接写出的值.
(1)、试说明;(2)、若点坐标为 , 点坐标为 , 请直接写出与之间的数量关系;(3)、如图2所示,过点作线段 , 交轴正半轴于点 , 交轴负半轴于点 , 使得点为中点,且 , 绕着顶点旋转直角 , 使得一边交轴正半轴于点 , 另一边交轴正半轴于点 , 此时,和是否还相等,请说明理由;(4)、在(3)条件下,请直接写出的值.