吉林省四平市双辽市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个企业的标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. $2^{0}$ 的值为（）

A、－1 B、0 C、1 D、2

查看试题解析
3. 下列运算正确的是（）

A、（a³）²＝a⁵ B、（﹣2a）³＝﹣6a³ C、a⁶÷a²＝a³ D、a^﹣1 $= \frac{1}{a}$ （a≠0）

查看试题解析
4. 下列等式中，从左到右的变形是因式分解的是（）

A、2x（x－1）＝2x²－2x B、x²－2x＋3＝x（x－2）＋3 C、（x＋y）²＝x²＋2xy＋y² D、－x²＋2x＝－x（x－2）

查看试题解析
5. 分式 $\frac{x - 4}{x + 2}$ 有意义的条件是（）

A、 $x = 2$ B、 $x \neq - 2$ C、 $x = - 2$ D、 $x = 4$

查看试题解析
6. 下列等式成立的是（）

A、 $\frac{2}{2 a + b} = \frac{1}{a + b}$ B、 $\frac{a}{- a + b} = - \frac{a}{a + b}$ C、 $\frac{1}{a} + \frac{2}{b} = \frac{3}{a + b}$ D、 $\frac{a b}{a b + b^{2}} = \frac{a}{a + b}$

查看试题解析

二、填空题

7. 某种计算机完成一次基本运算的时间约为 $0.0000000001 s$ ，把 $0.0000000001$ 用科学记数法可以表示为.

查看试题解析
8. 如图，在 $Δ A B C$ 和 $Δ A D C$ 中， $A B ⊥ B C$ ， $A D ⊥ D C$ ，只需添加一个条件即可证明 $Δ A B C ≌ Δ A D C$ ，这个条件可以是（写出一个即可）.

查看试题解析
9. 如图，在平面直角坐标系中， $△ O A B$ 的顶点坐标分别是 $A (- 6 ， 0) ， B (0 ， 4) ， △ O A B ≌ △ O A B$ ，若点 $A$ 在x轴上，则点 $B$ 的坐标是．

查看试题解析
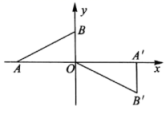10. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D、E可在槽中滑动．若∠BDE=75°，则∠CDE的度数是

查看试题解析
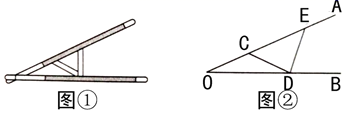11. 计算：（﹣0.25）²⁰²¹×4²⁰²²＝．

查看试题解析
12. 已知x²＋2（m－1）x＋16是完全平方式，则m的值为．

查看试题解析
13. 若 $a + \frac{1}{a} = 3$ ，则 $a - \frac{1}{a} =$ ．

查看试题解析
14. 已知关于x的方程 $\frac{2 x + m}{x - 2}$ ＝3的解是正数，则m的取值范围为．

查看试题解析

三、解答题

15. 计算：（2m²n^﹣2）²•3m^﹣3n³ ．

查看试题解析
16. 计算：（x﹣1）（x+3）﹣x（x﹣2）

查看试题解析
17. 分解因式： $x^{2} y - 9 y$ ．

查看试题解析
18. 化简： $\frac{2}{a^{2} + 2 a} + \frac{1}{a + 2}$ ．

查看试题解析
19. 如图，在△ABC 中，AB=AC，CD是∠ACB的平分线，DE∥BC，交AC于点 E．

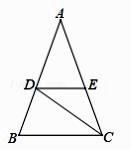(1)、求证：DE=CE．

(2)、若∠CDE=35°，求∠A 的度数．

查看试题解析
20. 计算：[（2x+y）（2x﹣y）﹣5x（x+2y）+ $(x + 2 y)^{2}$ ]÷（﹣3y）．

查看试题解析
21. 解方程： $\frac{3}{2} - \frac{1}{3 x - 1} = \frac{5}{6 x - 2}$ ．

查看试题解析
22. 如图，将一个边长为a+b的正方形图形分割成四部分（两个正方形和两个长方形），请认真观察图形，解答下列问题：

(1)、根据图中条件，请用两种方法表示该图形的总面积（用含a、b的代数式表示出来）；

(2)、如果图中的a，b（a＞b）满足a²+b²＝57，ab＝12，求a+b的值．

查看试题解析
23. 先化简（ $\frac{x^{2}}{x + 1}$ －x＋1）÷ $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，再从－1，0，1中选择合适的x值代入求值．

查看试题解析
24. 如图，四边形ABCD的对角线AC、BD相交于点E，若△ABC为等边三角形，AD⊥AB，AD＝DC＝4．

(1)、求证：BD垂直平分AC；

(2)、求BE的长；

(3)、若点F为BC的中点，请在BD上找出一点P，使PC+PF取得最小M值；PC+PF的最小值为（直接写出结果）．

查看试题解析
25. 某校田径队的小明同学参加了两次有氧耐力训练，每一次训练内容都是在400米环形跑道上慢跑10圈．若第二次慢跑速度比第一次慢跑速度提高了20%，则第二次比第一次提前5分钟跑完．

(1)、小勇同学一次有氧耐力训练慢跑是米；

(2)、小勇同学两次慢跑的速度各是多少？

查看试题解析
26. 如图，在△ABC中，AB＝AC，∠BAC＝30°，点D是△ABC内一点，DB＝DC，∠DCB＝30°，点E是BD延长线上一点，AE＝AB．

(1)、求∠ADB的度数；

(2)、线段DE，AD，DC之间有什么数量关系？请说明理由．（提示：在线段DE上截取线段EM＝BD，连接线段AM或者在线段DE上截取线段DM＝AD连接线段AM）．

查看试题解析