吉林省吉林市龙潭区2020-2021学年八年级上学期期末数学试题
试卷更新日期:2022-01-20 类型:期末考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为( )A、4cm B、6cm C、4cm或8cm D、8cm3. 小明上网查得新冠肺炎病毒的直径大约是106纳米,已知1纳米=0.000001毫米,试用科学记数法表示106纳米,下列正确的是( ).A、10.6×10﹣7米 B、1.06×10-7米 C、10.6×10﹣6米 D、1.06×10﹣6米4. 下列计算正确的是( )A、x2+x2=x4 B、2x3﹣x3=x3 C、x2•x3=x6 D、(x2)3=x55. 如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )
2. 若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为( )A、4cm B、6cm C、4cm或8cm D、8cm3. 小明上网查得新冠肺炎病毒的直径大约是106纳米,已知1纳米=0.000001毫米,试用科学记数法表示106纳米,下列正确的是( ).A、10.6×10﹣7米 B、1.06×10-7米 C、10.6×10﹣6米 D、1.06×10﹣6米4. 下列计算正确的是( )A、x2+x2=x4 B、2x3﹣x3=x3 C、x2•x3=x6 D、(x2)3=x55. 如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )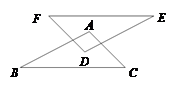 A、AB=DE B、∠B=∠E C、EF=BC D、EF//BC6. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角的平分线交于E点,连接AE,则∠AEC的度数是( )
A、AB=DE B、∠B=∠E C、EF=BC D、EF//BC6. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角的平分线交于E点,连接AE,则∠AEC的度数是( ) A、45° B、40° C、35° D、30°
A、45° B、40° C、35° D、30°二、填空题
-
7. 在△ABC中,已知∠B是∠A的2倍,∠C比∠A大20°,则∠A= .8. 已知2x+5y+3=0,求4x·32y = .9. 在边长为a的正方形中挖去一个边长为b的小正方形(其中a>b)(如图①),把余下的部分拼成一个长方形(如图②),根据两个图形中阴影部分的面积相等,可以验证的乘法公式是 .
 10. 分解因式4x2﹣4x+1=.11. 如图,在等边△ABC中,AD⊥BC,AD=AE,则∠EDC= .
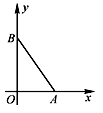
10. 分解因式4x2﹣4x+1=.11. 如图,在等边△ABC中,AD⊥BC,AD=AE,则∠EDC= . 12. 若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=13. 已知分式的值为0,那么x的值是 .14. 如图,在平面直角坐标系中,A(3,0),B(0,4),连接AB,在平面直角坐标系中找一点C,使△AOC与△AOB全等,则C点的坐标为
12. 若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=13. 已知分式的值为0,那么x的值是 .14. 如图,在平面直角坐标系中,A(3,0),B(0,4),连接AB,在平面直角坐标系中找一点C,使△AOC与△AOB全等,则C点的坐标为.
三、解答题
-
15. 化简:a(a﹣2b)+(a+b)2 .16. 解方程:17. 观察下面两个图形,解答下列问题:
 (1)、其中是轴对称图形的为(填序号);(2)、用尺规作图的方法画出其中轴对称图形的对称轴.(要求:保留作图痕迹,不写作法)18. 如图,△ABC中,D是边BC的中点,过点C作CE∥AB,交AD的延长线于点E.求证:AB=CE.
(1)、其中是轴对称图形的为(填序号);(2)、用尺规作图的方法画出其中轴对称图形的对称轴.(要求:保留作图痕迹,不写作法)18. 如图,△ABC中,D是边BC的中点,过点C作CE∥AB,交AD的延长线于点E.求证:AB=CE. 19. 先化简 ,再从0,1,2中选取一个合适的x的值代入求值.20. 已知A(-1,3),B(4,2),C(2,-1).
19. 先化简 ,再从0,1,2中选取一个合适的x的值代入求值.20. 已知A(-1,3),B(4,2),C(2,-1). (1)、在平面直角坐标系中,画出△ABC及△ABC关于y轴的对称图形△A1B1C1;(2)、P为x轴上一点,请在图中标出使△PAB的周长最小时的点P,并根据图象直接写出此时点P的坐标 .21. 将四个数a,b,c,d排列成2行,2列,记作 , 定义=ad-bc,上述记号就叫2阶行列式.(1)、根据定义,化简;(2)、请将(1)中的化简结果因式分解;(3)、请直接写出(1)中化简结果有最 值(填“大”或“小”),是 .22. 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连结BE.请找出一对全等三角形,并说明理由.
(1)、在平面直角坐标系中,画出△ABC及△ABC关于y轴的对称图形△A1B1C1;(2)、P为x轴上一点,请在图中标出使△PAB的周长最小时的点P,并根据图象直接写出此时点P的坐标 .21. 将四个数a,b,c,d排列成2行,2列,记作 , 定义=ad-bc,上述记号就叫2阶行列式.(1)、根据定义,化简;(2)、请将(1)中的化简结果因式分解;(3)、请直接写出(1)中化简结果有最 值(填“大”或“小”),是 .22. 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连结BE.请找出一对全等三角形,并说明理由. 23. 下面是某同学对多项式(x2+2x)(x2+2x+2)+1进行因式分解的过程
23. 下面是某同学对多项式(x2+2x)(x2+2x+2)+1进行因式分解的过程解:设x2+2x=y,
原式 =y(y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2+2x+1)2 (第四步)
(1)、该同学第二步到第三步运用了因式分解的( )A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式(2)、该同学在第四步将y用所设中的含x的代数式代换,这个结果是否分解到最后?. (填“是”或“否”)如果否,直接写出最后的结果
(3)、请你模仿以上方法尝试对多项式(x2﹣4x+3)(x2﹣4x+5)+1进行因式分解.24.(1)、探究:
如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.请直接写出线段BD,DE,CE之间的数量关系是 .
(2)、拓展:如图(2),将探究中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问探究中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)、应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,请直接写出△DEF的形状是 .
25. 用电脑程序控制小型赛车进行50m比赛,“畅想号”和“和谐号”两辆赛车进入了决赛,比赛前的练习中,两辆车从起点同时出发,“畅想号”到达终点时,“和谐号”离终点还差3m.已知“畅想号”的平均速度为2.5m/s.(1)、求“和谐号”的平均速度;(2)、如果两车重新开始比赛,“畅想号”从起点向后退3m,两车同时出发,两车能否同时到达终点?若能,求出两车到达终点的时间;若不能,请说明理由,并重新调整一辆车的平均速度,使两车能同时到达终点.(计算过程中如遇到近似数,请精确到0.001)26. 如图,△ABC中,AB=AC=8厘米,BC=6厘米,点D为AB的中点.动点P在线段BC上以2厘米/秒的速度向点C运动,同时,动点Q在线段CA上由点C向点A运动,连接DP,PQ.设点P运动的时间为t秒,回答下列问题: (1)、当点Q的运动速度为厘米/秒时,△BPD和△CPQ全等;(2)、若动点P的速度不变,同时动点Q以5厘米/秒的速度出发,两个点运动方向不变,沿△ABC的三边运动.
(1)、当点Q的运动速度为厘米/秒时,△BPD和△CPQ全等;(2)、若动点P的速度不变,同时动点Q以5厘米/秒的速度出发,两个点运动方向不变,沿△ABC的三边运动.①请求出两点首次相遇时的t值,并说明此时两点在△ABC的哪一条边上;
②在P、Q两点首次相遇前,能否得到以PQ为底的等腰△APQ?如果能,请直接写出t值;如果不能,请说明理由.