2022年苏科版初中数学《中考一轮复习》专题五 图形的变换 5.4 图形的相似
试卷更新日期:2022-01-20 类型:一轮复习
一、单选题
-
1. 下列各组中的四条线段,能构成比例线段的是( )A、1cm,2cm,4cm,6cm B、2cm,4cm,0.4cm,7cm C、3cm,9cm,18cm,6cm D、3cm,4cm,5cm,6cm2. 已知 是 的黄金分割点( ),若 ,则BC的长为( )A、( ) B、( ) C、( ) D、( )3. 如图,每个小方格的边长都是1,则下列图中三角形(阴影部分)与相似的是( )
 A、
A、 B、
B、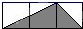 C、
C、 D、
D、 4. 如图,点D,E是△ABC中AB边上的点,△CDE是等边三角形,且∠ACB=120°,则下列结论中正确的是( )
4. 如图,点D,E是△ABC中AB边上的点,△CDE是等边三角形,且∠ACB=120°,则下列结论中正确的是( ) A、CD2=AD•BE B、BC2=BE•BD C、AC2=AD•AE D、AC•BC=AE•BD5. 如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A、CD2=AD•BE B、BC2=BE•BD C、AC2=AD•AE D、AC•BC=AE•BD5. 如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( ) A、5b B、3b C、b D、b6. 如图,在等腰△ABC中,∠ABC=∠ACB=α,BC=12,点D是边AB上一点,且BD=4,点P是边BC上一动点,作∠DPE=α,射线PE交边AC于点E , 当CE=9时,则满足条件的P点的个数是( )
A、5b B、3b C、b D、b6. 如图,在等腰△ABC中,∠ABC=∠ACB=α,BC=12,点D是边AB上一点,且BD=4,点P是边BC上一动点,作∠DPE=α,射线PE交边AC于点E , 当CE=9时,则满足条件的P点的个数是( )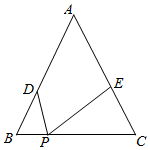 A、1 B、2 C、3 D、以上都有可能7. 如图在△ABC外任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得到△DEF,则下列说法正确的个数是( )
A、1 B、2 C、3 D、以上都有可能7. 如图在△ABC外任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得到△DEF,则下列说法正确的个数是( )①△ ABC与 △DEF是位似图形;② △ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
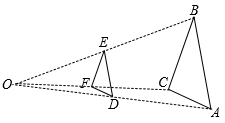 A、1个 B、2个 C、3个 D、4个8. 如图,△ABC中,点D为边BC上的点,点E、F分别是边AB、AC上两点,且EF∥BC,若AE:EB=m,BD:DC=n,则( )
A、1个 B、2个 C、3个 D、4个8. 如图,△ABC中,点D为边BC上的点,点E、F分别是边AB、AC上两点,且EF∥BC,若AE:EB=m,BD:DC=n,则( ) A、m>1,n>1,则2S△AEF>S△ABD B、m<1,n<1,则2S△AEF>S△ABD C、m>1,n<1,则2S△AEF<S△ABD D、m<1,n>1,则2S△AEF<S△ABD9. 在平面直角坐标系中,点A是双曲线上任意一点,连接 , 过点O作的垂线与双曲线交于点 , 连接 . 已知 , 则( )
A、m>1,n>1,则2S△AEF>S△ABD B、m<1,n<1,则2S△AEF>S△ABD C、m>1,n<1,则2S△AEF<S△ABD D、m<1,n>1,则2S△AEF<S△ABD9. 在平面直角坐标系中,点A是双曲线上任意一点,连接 , 过点O作的垂线与双曲线交于点 , 连接 . 已知 , 则( ) A、 B、 C、 D、10. 在正方形ABCD中,AB=2,E是BC的中点,在BC延长线上取点F使EF=ED,过点F作FG⊥ED交ED于点M,交AB于点G,交CD于点N,以下结论中:①tan∠GFB= ;②NM=NC;③ ;④S四边形GBEM= .正确的个数是( )
A、 B、 C、 D、10. 在正方形ABCD中,AB=2,E是BC的中点,在BC延长线上取点F使EF=ED,过点F作FG⊥ED交ED于点M,交AB于点G,交CD于点N,以下结论中:①tan∠GFB= ;②NM=NC;③ ;④S四边形GBEM= .正确的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 在 中, , 分别交 、 于点 、 ,已知 , , ,则 .12. 已知 , 则.13. 如图,小明周末晚上陪父母在锦江绿道上散步,他由灯下A处前进4米到达B处时,测得影子BC长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子DE长为米.
 14. 如图,在四边形ABCD中,∠A=∠D=120°,AB=6、AD=4,点E、F分别在线段AD、DC上(点E与点A、D不重合),若∠BEF=120°,AE=x、DF=y,则y关于x的函数关系式为
14. 如图,在四边形ABCD中,∠A=∠D=120°,AB=6、AD=4,点E、F分别在线段AD、DC上(点E与点A、D不重合),若∠BEF=120°,AE=x、DF=y,则y关于x的函数关系式为 15. 如图,在矩形ABCD中,AB=6,BC , 点N在边AD上,ND=2,点M在边BC上,BM=1,点E在DC的延长线上,连接AE,过点E作EF⊥AE交直线MN于点F,当AE=EF时,DE的长为 .
15. 如图,在矩形ABCD中,AB=6,BC , 点N在边AD上,ND=2,点M在边BC上,BM=1,点E在DC的延长线上,连接AE,过点E作EF⊥AE交直线MN于点F,当AE=EF时,DE的长为 .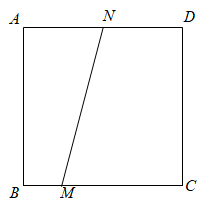 16. 如图,四边形ABCD和四边形ABEC均为平行四边形,点H为BE的中点,连接DH , 分别交AC , BC于点F , G , 已知平行四边形ABCD的面积为8cm2 , 则△ADF的面积为 cm2 .
16. 如图,四边形ABCD和四边形ABEC均为平行四边形,点H为BE的中点,连接DH , 分别交AC , BC于点F , G , 已知平行四边形ABCD的面积为8cm2 , 则△ADF的面积为 cm2 . 17. 如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M, EG的延长线交AB于点H,若∠BAC=60°,则 =
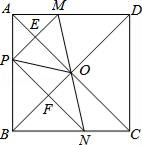
17. 如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M, EG的延长线交AB于点H,若∠BAC=60°,则 = 18. 如图,在正方形 中,点 是 上一动点(不与 , 重合),对角线 、 相交于点 ,过点 分别作 、 的垂线,分别交 、 于点 、 ,交 、 于点 、 .下列结论:① ;② ;③ ;④ ;⑤当 时,点 是 的中点.
18. 如图,在正方形 中,点 是 上一动点(不与 , 重合),对角线 、 相交于点 ,过点 分别作 、 的垂线,分别交 、 于点 、 ,交 、 于点 、 .下列结论:① ;② ;③ ;④ ;⑤当 时,点 是 的中点.其中正确的结论有.
三、解答题
-
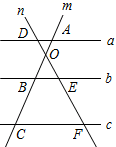
19. 如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
 20. 如图,已知∠1=∠2,∠AED=∠C,
20. 如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE
 21. 如图,四边形 , , 均是正方形,且 , , , 在同一直线上,连接 , ,则 的度数为多少?
21. 如图,四边形 , , 均是正方形,且 , , , 在同一直线上,连接 , ,则 的度数为多少? 22. 在四边形ABCD中, , , , , 的平分线分别交AD、AC于点E、F,求 的值.
22. 在四边形ABCD中, , , , , 的平分线分别交AD、AC于点E、F,求 的值. 23. 如图,在△ABC中,EFCD,DEBC.
23. 如图,在△ABC中,EFCD,DEBC. (1)、求证:AF:FD=AD:DB;(2)、若AB=30,AD:BD=2:1,请直接写出DF的长.24. 如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
(1)、求证:AF:FD=AD:DB;(2)、若AB=30,AD:BD=2:1,请直接写出DF的长.24. 如图所示,AD、BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯C下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
①计算小亮在路灯D下的影长;
②计算建筑物AD的高.
25. 如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.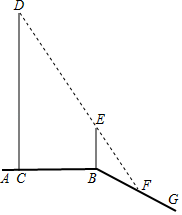 26. 如图,正方形ABCD的边长是6,E,F分别是直线BC,直线CD上的动点,当点E在直线BC上运动时,始终保持AE⊥EF.
26. 如图,正方形ABCD的边长是6,E,F分别是直线BC,直线CD上的动点,当点E在直线BC上运动时,始终保持AE⊥EF. (1)、求证:Rt△ABE∽Rt△ECF;(2)、当点E在边BC上,四边形ABCF的面积等于20时,求BE的长;(3)、当点E在直线BC上时,△AEF和△CEF能相似吗?若不能,说明理由,若能请直接写出此时BE的长.27. 如图,已知抛物线经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点.
(1)、求证:Rt△ABE∽Rt△ECF;(2)、当点E在边BC上,四边形ABCF的面积等于20时,求BE的长;(3)、当点E在直线BC上时,△AEF和△CEF能相似吗?若不能,说明理由,若能请直接写出此时BE的长.27. 如图,已知抛物线经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点. (1)、求抛物线的解析式.(2)、过点P与y轴平行的直线l与直线AB,AC分别交于点E,F,当点P在何处时,四边形AECP的面积最大,最大是多少?(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.28. 如图,四边形ABCD中,AD//BC, , , ,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作 于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒( )
(1)、求抛物线的解析式.(2)、过点P与y轴平行的直线l与直线AB,AC分别交于点E,F,当点P在何处时,四边形AECP的面积最大,最大是多少?(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C,P,Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.28. 如图,四边形ABCD中,AD//BC, , , ,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.当其中一个动点到达终点时,另一个动点也随之停止运动.过点N作 于点P,连接AC交NP于点Q,连接MQ,设运动时间为t秒( )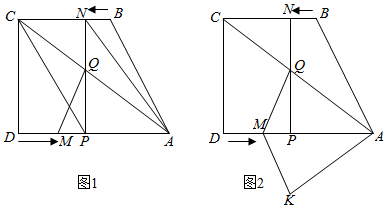 (1)、连接AN,CP,当t为何值时,四边形ANCP为平行四边形;(2)、设四边形DMQC的面积为y,求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;(4)、将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.
(1)、连接AN,CP,当t为何值时,四边形ANCP为平行四边形;(2)、设四边形DMQC的面积为y,求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形DMQC的面积与△ABC的面积相等?若存在,求出t的值;若不存在,请说明理由;(4)、将△AQM沿AD翻折,得到△AKM.在运动过程中,是否存在某时刻t,使四边形AQMK为菱形,若存在,求出t的值;若不存在,请说明理由.