湘教版初中数学七年级下册2.2.2完全平方公式同步练习

试卷更新日期：2022-01-20 类型：同步测试

进入出卷网下载

一、单选题

1. 如果 $x$ ²＋2m $x$ ＋16是一个完全平方式，则m的值是（）

A、4 B、8 C、 $\pm$ 4 D、 $\pm$ 8

查看试题解析
2. 若 $a^{2} + a b = 7 + m$ ， $b^{2} + a b = 9 - m$ .则 $a + b$ 的值为（）

A、 $\pm 4$ B、4 C、 $\pm 2$ D、2

查看试题解析
3. 已知M＝3x²－x＋3，N＝2x²＋3x－1，则M、N的大小关系是（）

A、M≥N B、M＞N C、M≤N D、M＜N

查看试题解析
4. 若 $x^{2} - k x y + 9 y^{2}$ 是一个完全平方式，则常数k的值为 $($ $)$

A、6 B、 $- 6$ C、 $\pm 6$ D、无法确定

查看试题解析
5. 若多项式 $9 x^{2} - m x + 4$ 是一个完全平方式，则m的值为（）

A、12 B、±12 C、6 D、±6

查看试题解析
6. 下列计算正确的是（）

A、 $(x + 2 y) (x - 2 y) = x^{2} - 2 y^{2}$ B、 $(x - y) (- x - y) = - x^{2} - y^{2}$ C、 ${(x - y)}^{2} = x^{2} - 2 x y + y^{2}$ D、 ${(x + y)}^{2} = x^{2} + y^{2}$

查看试题解析
7. 如图，4张边长分别为 $a$ 、 $b$ 的长方形纸片围成一个正方形，从中可以得到的等式是（）

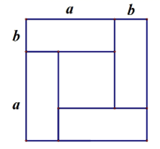A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 ${(a + b)}^{2} - {(a - b)}^{2} = 4 a b$

查看试题解析
8. 已知（a+b）²=8，（a-b）²=2，则a²+b²的值是（）

A、3 B、5 C、6 D、10

查看试题解析
9. 将 $98^{2}$ 变形正确的是（）

A、 $98^{2} = 90^{2} + 8^{2}$ B、 $98^{2} = 90^{2} - 90 \times 8 + 8^{2}$ C、 $98^{2} = 100^{2} - 2 \times 100 \times 2 + 2^{2}$ D、 $98^{2} = (100 + 2) (100 - 2)$

查看试题解析
10. 如果 $x^{2} + m x + 4$ 是一个完全平方式，则 $m$ 等于（）

A、-4 B、2 C、4 D、±4

查看试题解析
11. 将图1中四个阴影小正方形拼成边长为2所示，根据两个图形中阴影部分面积间的关系，可以验证下列哪个乘法公式（）

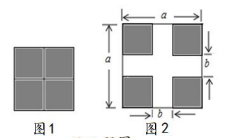A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 ${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

查看试题解析
12. 如图，在长方形ABCD中，AB<BC，点P为长方形内部一点，过点P分别做PE⊥BC于点E、PF⊥CD于点F，分别以PF、CF为边做作正方形PMNF，正方形GHCF，若两个正方形的面积之和为 $\frac{73}{4}$ ，EH= $\frac{5}{2}$ ，BE=DF=2，则长方形ABCD的面积为（）

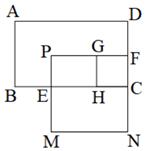A、17 B、21 C、24 D、28

查看试题解析

二、填空题

13. 已知 $x - \frac{1}{x} = 7$ ，则 $x^{2} + \frac{1}{x^{2}} =$ ．

查看试题解析
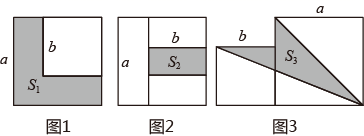
14. 已知 ${(2021 - a)}^{2} + {(a - 2020)}^{2} = 7$ ，则代数式 $(2021 - a) (a - 2020)$ 的值是．

查看试题解析
15. 如果（a+　）²＝a²+6ab+9b² ，那么括号内可以填入的代数式是．（只需填写一个）

查看试题解析
16. 若二次三项式x²﹣kx＋16是一个完全平方式，则k的值是.

查看试题解析
17. 若一个整数能表示成 $a^{2} + b^{2}$ （a、b为整数）的形式，则称这个数为“完美数”，例如：因为 $5 = 2^{2} + 1$ ，所以5是一个完美数.已知 $M = x^{2} + 4 y^{2} + 4 x - 12 y + k$ （x、y是整数，k是常数），要使M为“完美数”，则k的值为.

查看试题解析
18. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为 $S_{1}$ ；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为 $S_{2}$ .若 $a + b = 8 ， a b = 10$ ，则 $S_{1}$ ＋ $S_{2}$ ＝；当 $S_{1}$ ＋ $S_{2}$ ＝40时，则图3中阴影部分的面积 $S_{3} =$ .

查看试题解析

三、计算题

19. 计算：(2x+y)²+(x-y)(x+y)-5x(x-y)

查看试题解析
20. 化简：(2m+3n)²-(2m+n)(2m-n)

查看试题解析

四、解答题

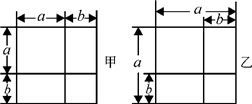
21. 利用图形中面积的等量关系可以得到某些数学公式．例如，根据图甲，我们可以得到两数和的平方公式：（a+b）²=a²+2ab+b² ．你根据图乙能得到的数学公式是怎样的？写出得到公式的过程．

查看试题解析
22. 已知 $a ， b ， c$ 是 $△ A B C$ 的三边的长，且满足 $a^{2} + 2 b^{2} + c^{2} - 2 b (a + c) = 0$ ，试判断此三角形的形状.

查看试题解析
23. 如图摆放两个正方形，它们的周长之和为24、面积之和为20，求阴影部分的面积.

查看试题解析

五、综合题

24. 已知a+b＝6，ab＝2，求下列各式的值

(1)、a²+b²；

(2)、（a﹣b）².

查看试题解析
25.

(1)、在下列横线上用含有a，b的代数式表示相应图形的面积.

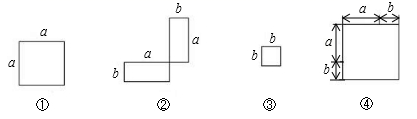
①a²；②. ③b² ； ④.

(2)、请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达：.

(3)、利用（2）的结论计算10.23²+20.46×9.77+9.77²的值.

查看试题解析
26.

(1)、填写下表：

a，b的值

${(a - b)}^{2}$

$a^{2} - 2 a b + b^{2}$

a=4，b=2

4

a=-1，b=3

16

a=-2，b=-5

(2)、比较表中两式的计算结果，你发现 ${(a - b)}^{2}$ 与 $a^{2} - 2 a b + b^{2}$ 有什么关系？

(3)、利用你发现的结论，求2 019²-4 038×2 017+2 017²．

查看试题解析
27. 将完全平方公式（a±b）²＝a²±2ab+b²作适当的变形，可以解决很多的数学问题.请你观察、思考并解决下列问题：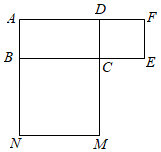

(1)、若m+n＝7，m²+n²＝25，且m＜n，求m﹣n的值；

(2)、如图，长方形ABCD的周长是160米，以BC、CD为边分别向外作正方形BCMN、正方形DCEF，若这两块正方形的面积和为4000平方米，求长方形ABCD的面积.

查看试题解析
28. 阅读：若 $x$ 满足 $(60 - x) (x - 40) = 30$ ，求 ${(60 - x)}^{2} + {(x - 40)}^{2}$ 的值，
解：设 $(60 - x) = a$ ， $(x - 40) = b$ ，则 $(60 - x) (x - 40) = a b =$ ______， $a + b = (60 - x) + (x - 40) =$ ______，所以 ${(60 - x)}^{2} + {(x - 40)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b =$ ______.

请仿照上例解决下面的问题：

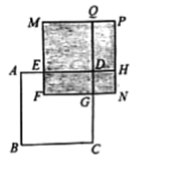(1)、补全题目中横线处：

(2)、已知 $(30 - x) (x - 20) = - 10$ ，求 ${(30 - x)}^{2} + {(x - 20)}^{2}$ 的值；

(3)、若 $x$ 满足 ${(2023 - x)}^{2} + {(2022 - x)}^{2} = 2021$ ，求 $(2023 - x) (x - 2022)$ 的值；

(4)、如图，正方形 $A B C D$ 的边长为 $x$ ， $A E = 10$ ， $C G = 25$ ，长方形 $E F G D$ 的面积是400，四边形 $N G D H$ 和 $M E D Q$ 都是正方形， $P Q D H$ 是长方形，求图中阴影部分的面积（结果必须是一个具体数值）.

查看试题解析

a，b的值	${(a - b)}^{2}$	$a^{2} - 2 a b + b^{2}$
a=4，b=2	4
a=-1，b=3		16
a=-2，b=-5