湘教版初中数学七年级下册2.2.1平方差公式同步练习

试卷更新日期：2022-01-20 类型：同步测试

进入出卷网下载

一、单选题

1. 从边长为a的正方形内去掉一个边长为b的小正方形（如图1），然后将剩余部分剪拼成一个矩形（如图2），上述操作所能验证的等式是（　　）

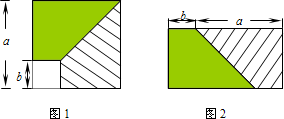A、（a-b）2=a2-2ab+b2 B、a2-b2=（a+b）（a-b） C、（a+b）2=a2+2ab+b2 D、a2+ab=a（a+b）

查看试题解析
2.
如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分面积，可以验证下面一个等式是（）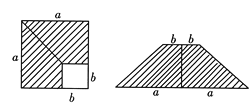

A、（a+b）²=a²+2ab+b² B、（a-b）²=a²-2ab+b² C、a²-b²=（a+b）（a-b） D、a²+b²=（a+b）（a-b）

查看试题解析
3. 记 $x = (1 + 2) (1 + 2^{2}) (1 + 2^{4}) (1 + 2^{8}) \dots (1 + 2^{n})$ ，且 $x + 1 = 2^{128}$ ，则 $n =$ （）．

A、128 B、32 C、64 D、16

查看试题解析
4. 下列乘法中，能应用平方差公式的是（）

A、（x﹣y）（y﹣x） B、（2x﹣3y）（3x+2y） C、（﹣x﹣y）（x+y） D、（﹣2x﹣3y）（3y﹣2x）

查看试题解析
5. 如图，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形，小佳将阴影部分通过剪拼，拼成了图①、图②、图③三种新的图形，其中能够验证平方差公式的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
6. 下列多项式中，能用平方差公式分解因式的是（）

A、a²-1 B、-a²-1 C、a²+1 D、a²+a

查看试题解析
7. 下列式子中，能用平方差公式运算的是（）

A、 $(x - y) (x + y)$ B、 $(- x + y) (y - x)$ C、 $(x + y) (- x - y)$ D、 $(x - y) (- x + y)$

查看试题解析
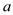8. 如图，在边长为的正方形中挖掉一个边长为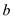的小正方形（，把余下部分剪拼成长方形如右图，通过计算两个图形（阴影部分）的面积，验证了一个等式，这个等式是（）

A、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$ B、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
9. 下列多项式的乘法可以运用平方差公式计算的是（）

A、（2x+3y）（2y﹣3x） B、（﹣2x﹣3y）（2x+3y） C、（﹣2x+3y）（2x﹣3y） D、（2x﹣3y）（﹣2x﹣3y）

查看试题解析
10. 若（2021²﹣4）（2020²﹣4）＝2023×2019×2018m ，则m的值是（）

A、2020 B、2021 C、2022 D、2024

查看试题解析
11. 在下列多项式的乘法中，不能用平方差公式计算的是（）

A、(a＋b)(a－b) B、(x－2y)(－x＋2y) C、(x－2y)(－x－2y) D、( $\frac{1}{2}$ x－y)(y＋0.5x)

查看试题解析
12. 下列各式能用平方差公式分解因式的是（）

A、m²+n² B、4x²﹣（﹣y²） C、﹣4a²﹣b² D、﹣9x²+4y²

查看试题解析

二、填空题

13. 100²﹣99²＋98²﹣97²＋96²﹣95²＋…＋2²﹣1²＝．

查看试题解析
14. 根据公式x²﹣y²＝（x+y）（x﹣y）来解题有时能起到简化计算的效果.比如计算50²﹣49＝（50+49）×（50﹣49）＝99×1＝99，根据这种方法计算（ $\frac{9}{11}$ ）²﹣（ $\frac{2}{11}$ ）²结果是

查看试题解析
15. 计算( $\sqrt{7}$ +1)( $\sqrt{7}$ -1)的结果等于

查看试题解析
16. 计算：(2+ $\sqrt{3}$ )(2- $\sqrt{3}$ )=

查看试题解析
17. 已知 $x - 2 y = 1$ ，则 $x^{2} - 4 y - 4 y^{2} =$ .

查看试题解析
18. 数学活动课上，小明同学尝试将正方形纸片剪去一个小正方形，剩余部分沿虚线剪开，拼成新的图形。现给出下列3种不同的剪、拼方案，其中能够验证平方差公式的方案是。(请填上正确的序号)

查看试题解析

三、计算题

19. （a﹣2b＋c）（a＋2b﹣c）．

查看试题解析
20. 简便计算：2³×5⁴+29×31．

查看试题解析

四、解答题

21. 算式2(3+1)(3²+1)(3⁴+1)(3⁸+1)(3¹⁶+1)(3³²+1)+1计算的结果个位是几？

查看试题解析
22. 老师在黑板上写了三个算式，希望同学们认真观察，发现规律.请你结合这些算式，解答下列问题：
请观察以下算式：

① $3^{2} - 1^{2} = 8 \times 1$ ；

② $5^{2} - 3^{2} = 8 \times 2$ ；

③ $7^{2} - 5^{2} = 8 \times 3$ ；

……

试写出符合上述规律的第五个算式；

验证：设两个连续奇数为2n+1， $2 n - 1$ (其中 $n$ 为正整数)，并说明它们的平方差是8的倍数；

查看试题解析
23. 原有长方形绿地一块，现进行如下改造，将长减少2m，将宽增加2m，改造后得到一块正方形绿地，它的面积是原绿地面积的2倍，求改造后正方形绿地的面积.

查看试题解析
24. 当n为自然数时，(n+7)²-(n-5)²能被24整除吗？说明理由．

查看试题解析
25. 分解因式: ${(3 m - 1)}^{2} - {(2 m - 3)}^{2}$ .

查看试题解析

五、综合题

26.

(1)、例：代数式

{(a + b)}^{2}

表示

a

、

b

两数和的平方，仿照上例填空：代数式

(a + b) (a - b)

表示

(2)、试计算

a

、

b

取不同数值时，

a^{2} - b^{2}

及

(a + b) (a - b)

的值，填入表：

$a$ 、 $b$ 的值	当 $a = 3$ ， $b = 2$ 时	当 $a = - 5$ ， $b = 1$ 时	当 $a = - 2$ ， $b = - 5$ 时
$a^{2} - b^{2}$
$(a + b) (a - b)$

(3)、我的发现：；

(4)、用你发现的规律计算：

{78.35}^{2} - {21.65}^{2}

．

查看试题解析

27. 如图1，在一个边长为 $a$ 的正方形中，剪去一个边长为 $b$ 的小正方形，再将余下的部分拼成如图2所示的长方形．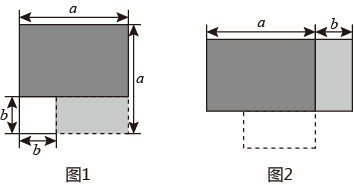

(1)、（观察）
比较两图中阴影部分的面积，可以得到等式：（用字母 $a$ ， $b$ 表示）；

(2)、（应用）
计算： $(x - 3) (x + 3) (x^{2} + 9)$ ；

(3)、（拓展）
已知 $2 m - n = 3$ ， $2 m + n = 4$ ，求 $8 m^{2} - 2 n^{2}$ 的值．

查看试题解析
28. 如图，边长为a的大正方形中有一个边长为b的小正方形，图2由图1中的阴影部分拼成的一个长方形.

(1)、设图1中阴影部分面积为S₁ ，图2中阴影部分面积为S₂ ，请用含a，b的代数式示：S₁= ， S₂= （只需表示，不必化简）；

(2)、以上结果可以验证哪个乘法公式？请写出这个乘法公式；

(3)、运用（2）中得到的公式，计算：2018²-2019×2017.

查看试题解析
29. 探究规律，解决问题：

(1)、化简： $(m - 1) (m + 1) =$ ， $(m - 1) (m^{2} + m + 1) =$ ．

(2)、化简： $(m - 1) (m^{3} + m^{2} + m + 1)$ ，写出化简过程．

(3)、化简： $(m - 1) (m^{n} + m^{n - 1} + m^{n - 2} + \dots + 1) =$ ．（n为正整数， $m^{n} + m^{n - 1} + m^{n - 2} + \dots + 1$ 为 $n + 1$ 项多项式）

(4)、利用以上结果，计算 $1 + 3 + 3^{2} + 3^{3} + \dots + 3^{100}$ 的值．

查看试题解析