湘教版初中数学七年级下册2.1.4多项式的乘法同步练习
试卷更新日期:2022-01-20 类型:同步测试
一、单选题
-
1. 计算 的结果为( )A、 B、 C、 D、
-
2. 如图是一栋楼房的平面图,下列式子中不能表示它的面积的是( )
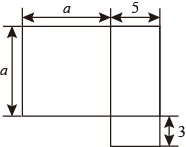 A、 B、(a+5)(a+3)-3a C、a(a+5)+15 D、
A、 B、(a+5)(a+3)-3a C、a(a+5)+15 D、 -
3. 如图,是一楼房的平面图,下列式子中不能表示它的面积的是( )
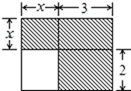 A、 B、 C、 D、
A、 B、 C、 D、 -
4. 如果计算( )( )的结果中不含关于 的一次项,那么 的值为( )A、- B、 C、-3 D、3
-
5. 若 的乘积中不含 项,则 的值为( )A、5 B、 C、 D、-5
-
6. 多项式x3﹣5x2﹣3x﹣y中,有一个因式为(x﹣5),则y的值为( )A、﹣15 B、15 C、﹣3 D、3
-
7. 已知无论x取何值,等式 恒成立,则关于代数式 的值有下列结论:①交换a,b的位置,代数式的值不变;②该代数式的值是非正数;③该代数式的值不会小于-2,上述结论正确的是( )A、①② B、①③ C、②③ D、①②③
-
8. 有足够多张如图所示的 类、 类正方形卡片和 类长方形卡片,如果要拼一个长为 、宽为 的大长方形,则需要 类卡片的张数为( )
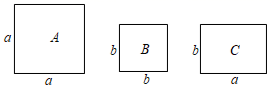 A、3 B、4 C、6 D、7
A、3 B、4 C、6 D、7 -
9. 已知 ,则b的值是( )A、-5 B、-2 C、2 D、3
-
10. 已知:(2021﹣a)(2020﹣a)=4,则(2021﹣a)2+(2020﹣a)2的值为( )A、7 B、8 C、9 D、12
-
11. 如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(a+b)的大长方形,则需要C类卡片( )
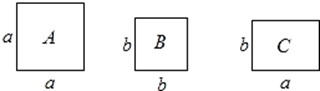 A、2张 B、3张 C、4张 D、5张
A、2张 B、3张 C、4张 D、5张 -
12. 如果(x﹣4)(x+3)=x2+mx﹣12,则m的值为( )A、1 B、﹣1 C、7 D、﹣7
二、填空题
-
13. 计算:4x(y﹣x)= .
-
14. 计算:(x2﹣3)(x2+5)= .
-
15. 如果两个多项式有公因式,则称这两个多项式为关联多项式,若x2﹣25与(x+b)2为关联多项式,则b=;若(x+1)(x+2)与A为关联多项式,且A为一次多项式,当A+x2﹣6x+2不含常数项时,则A为.
-
16. 若 = , b=
-
17. 若3x2+kx+4被3x﹣1除后余2,则k的值为 .
-
18. 用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为 , 的正方形和长为 宽为 的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为: .
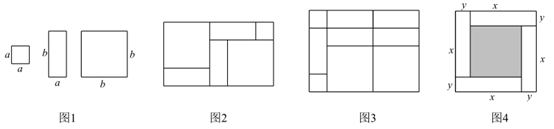 (1)、图3可以解释为等式:;(2)、要拼出一个两边长为 , 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论;
(1)、图3可以解释为等式:;(2)、要拼出一个两边长为 , 的长方形,先回答需要以下三种纸片各多少块,再用画图或整式乘法验证你的结论; 块,
块,  块,
块,  块(3)、如图4,大正方形的边长为 ,小正方形的边长为 ,若用 , ( )表示四个相同小长方形的两边长,以下关系式正确的是 (填序号).① ;② ;③ ;④ .
块(3)、如图4,大正方形的边长为 ,小正方形的边长为 ,若用 , ( )表示四个相同小长方形的两边长,以下关系式正确的是 (填序号).① ;② ;③ ;④ .
三、解答题
-
19. 计算(1)、(2)、(3)、
-
20. 若(x2+ax+8)(x2﹣3x+b)的乘积中不含x2和x3项,求a,b的值.
-
21. 已知m2﹣m﹣2=0,求代数式m(m﹣1)+(m+1)(m﹣2)的值.
-
22. 求代数式x(2x﹣1)﹣2(x﹣2)(x+1)的值,其中x=2017.
-
23. 仔细阅读下面例题.解答问题:
例题:已知二次三项式,x2-4x+m分解因式后有一个因式是(x+3).求另一个因式以及m的值.
解:方法:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n).则x2-4x+m=x2+(n+3)x+3n,∴ ,解得 ,∴另一个因式为(x-7),m的值为-21.
仿照以上方法解答:已知二次三项式8x2-14x-a分解因式后有一个因式是(2x-3).求另一个因式以及a的值.
-
24. 一些代数恒等式可以用平面几何图形的面积来表示,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用图1或图2等图形的面积来表示.
 (1)、请写出下图所表示的代数恒等式:;
(1)、请写出下图所表示的代数恒等式:; (2)、试画出一个几何图形,使它的面积能表示为:(a+b)(a+3b)=a2+4ab+3b2;(3)、请仿照上述方法另写一个含有a、b的代数恒等式,并画出与之对应的几何图形.
(2)、试画出一个几何图形,使它的面积能表示为:(a+b)(a+3b)=a2+4ab+3b2;(3)、请仿照上述方法另写一个含有a、b的代数恒等式,并画出与之对应的几何图形. -
25. 小红准备完成题目:计算(x2
 x+2)(x2﹣x).她发现第一个因式的一次项系数被墨水遮挡住了. (1)、她把被遮住的一次项系数猜成3,请你完成计算:(x2+3x+2)(x2﹣x);(2)、老师说:“你猜错了,这个题目的正确答案是不含三次项的.”请通过计算说明原题中被遮住的一次项系数是多少?
x+2)(x2﹣x).她发现第一个因式的一次项系数被墨水遮挡住了. (1)、她把被遮住的一次项系数猜成3,请你完成计算:(x2+3x+2)(x2﹣x);(2)、老师说:“你猜错了,这个题目的正确答案是不含三次项的.”请通过计算说明原题中被遮住的一次项系数是多少? -
26. 亮亮计算一道整式乘法的题(3x﹣m)(2x﹣5),由于亮亮在解题过程中,抄错了第一个多项式中m前面的符号,把“﹣”写成了“+”,得到的结果为6x2﹣5x﹣25.(1)、求m的值;(2)、计算这道整式乘法的正确结果.
-
27. 已知有甲、乙两个长方形,它们的边长如图所示,面积分别为S1 , S2.
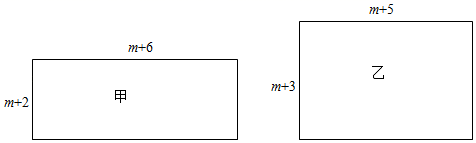 (1)、S1与S2的大小关系为:S1 S2.(2)、若一个正方形的周长与甲的周长相等.
(1)、S1与S2的大小关系为:S1 S2.(2)、若一个正方形的周长与甲的周长相等.①求该正方形的边长(用含m的代数式表示).
②若该正方形的面积为S3 , 试探究:S3与S2的差(即S3﹣S2)是否为常数?若为常数,求出这个常数,如果不是,请说明理由.
