黑龙江省齐齐哈尔市梅里斯达斡尔族区2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-01-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段，不能组成三角形的是（）

A、3，8，4 B、4，9，6 C、15，20，8 D、9，15，8

查看试题解析
2. 下列运算正确的是（）

A、（2x⁵）²=2x¹⁰ B、（﹣3）^﹣2= $\frac{1}{9}$ C、（a+1）²=a²+1 D、a²•a³=a⁶

查看试题解析
3. 下面有4个汽车标志图案，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列四个分式中，是最简分式的是（）

A、 $\frac{a^{2} + b^{2}}{a + b}$ B、 $\frac{x^{2} + 2 x + 1}{x + 1}$ C、 $\frac{2 a x}{3 a y}$ D、 $\frac{a^{2} - b^{2}}{a - b}$

查看试题解析
5. 人体中红细胞的直径约为0.0000077 m，用科学记数法表示数的结果是（）

A、0.77×10^－⁵ m B、0.77×10^－⁶ m C、7.7×10^－⁵ m D、7.7×10^－⁶ m

查看试题解析
6. 如图所示，在△ABC中，∠C=90°，AD平分∠BAC ， DE⊥AB于E ， DE=4，BC=9，则BD的长为（）

A、6 B、5 C、4 D、3

查看试题解析
7. 如图所示，线段AC的垂直平分线交线段AB于点D，∠A＝50°，则∠BDC＝（）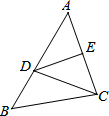

A、50° B、100° C、120° D、130°

查看试题解析
8. 如果 $x^{2} + (m - 2) x + 9$ 是个完全平方式，那么 $m$ 的值是（）

A、8 B、-4 C、±8 D、8或-4

查看试题解析
9. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是（）

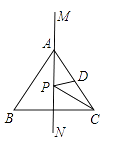A、30° B、15° C、20° D、35°

查看试题解析
10. 如图，在△ABC中，AB=AC ， D是BC的中点，连接AD ， E在BC的延长线上，连接AE ， ∠E=2∠CAD ，下列结论：
①AD⊥BC；②∠E=∠BAC；③CE=2CD；④AE=BE ．其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11.
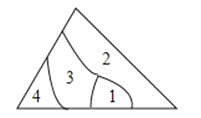
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块．

查看试题解析
12. 若有（x﹣3）⁰=1成立，则x应满足条件．

查看试题解析
13. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为零，则x的值为．

查看试题解析
14. 若正多边形的每一个内角为 $135^{\circ}$ ，则这个正多边形的边数是．

查看试题解析
15. 在等腰△ABC中，AB=AC ， ∠BAC=20°，点D在直线BC上，且CD=AC ，连接AD ，则∠ADC的度数为．

查看试题解析
16. 已知关于x的方程 $\frac{a x - 1}{x - 2} = \frac{1}{x - 2}$ 无解，则 $a =$ ．

查看试题解析
17. 如图，长方形ABCD中，AB=2cm，AD=1cm，在直线DA上，将长方形ABCD向右无滑动的滚动下去，（如①为第1次、②为第2次、③为第3次……）则第2022此滚动后得到的长方形最右侧边与CD边的距离为cm．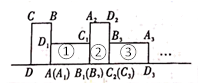

查看试题解析

三、解答题

18. 因式分解

(1)、 $- 3 x^{3} y^{2} + 6 x^{2} y^{3} - 3 x y^{4}$ ；

(2)、 $3 x (a - b) - 6 y (b - a)$ ．

查看试题解析
19. 解分式方程： $\frac{4}{x^{2} - 4} = \frac{3}{x + 2} + \frac{1}{x - 2}$

查看试题解析
20.

(1)、计算：4（x+1）²-（2x+3）（2x-3）

(2)、先化简，再求值 $\frac{a^{2} - 1}{a^{2} + 2 a + 1} \div \frac{a^{2} - a}{a + 1} - \frac{a - 1}{a}$ ，其中a=5．

查看试题解析
21. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系之后，△ABC的顶点均在格点上，点C的坐标为（5，1）．

(1)、画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；

(2)、连接OB、OC ，直接写出△OBC的面积．

查看试题解析
22. 如图，AE＝AD，∠ABE＝∠ACD，BE与CD相交于O．

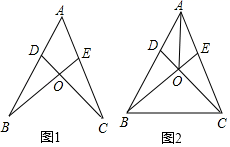(1)、如图1，求证：AB＝AC；

(2)、如图2，连接BC、AO，请直接写出图2中所有的全等三角形（除△ABE≌△ACD外）．

查看试题解析
23. 甲、乙两个工程队计划修建一条长15千米的乡村公路，已知甲工程队每天比乙工程队每天多修路0.5千米，乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍．

(1)、求甲、乙两个工程队每天各修路多少千米？

(2)、若甲工程队每天的修路费用为0.5万元，乙工程队每天的修路费用为0.4万元，要使两个工程队修路总费用不超过5.2万元，甲工程队至少修路多少天？

查看试题解析
24. 在Rt△ABC中，AB=AC，∠BAC=90°，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到线段AE．

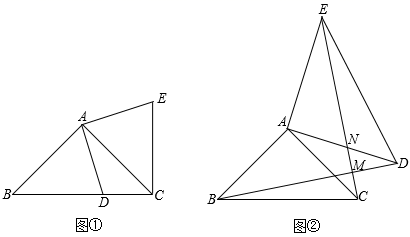(1)、探索：连接EC，如图①，试探索线段BC，CD，CE之间满足的等量关系，并证明结论；

(2)、如图②，在四边形ABCD中，∠ABC=∠ACB=45°，若BD=7，将边AD绕点A逆时针旋转90°得到线段AE．连接DE、CE，求线段CE的长．

(3)、AD与CE交于点N，BD与CE交于点M，在（2）的条件下，试探究BD与CE的位置关系，并加以证明

查看试题解析