黑龙江省大庆市杜尔伯特蒙古族自治县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-19 类型:期末考试
一、单选题
-
1. 如图下面图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 代数式 , , , 中,分式的个数为( )A、1 B、2 C、3 D、43. 若m<n,则下列各式正确的是( )A、﹣2m<﹣2n B、 C、1﹣m>1﹣n D、m2<n24. 下列多项式中能用平方差公式分解因式的是( )A、﹣a2﹣b2 B、x2+(﹣y)2 C、(﹣x)2+(﹣y)2 D、﹣m2+15. 下列不能判定一个四边形是平行四边形的是( )A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行另一组对边相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形6. 计算 的结果正确的是( )A、 B、 C、 D、7. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,△ABC的周长为18,AE = 3,则△ABD的周长( )
2. 代数式 , , , 中,分式的个数为( )A、1 B、2 C、3 D、43. 若m<n,则下列各式正确的是( )A、﹣2m<﹣2n B、 C、1﹣m>1﹣n D、m2<n24. 下列多项式中能用平方差公式分解因式的是( )A、﹣a2﹣b2 B、x2+(﹣y)2 C、(﹣x)2+(﹣y)2 D、﹣m2+15. 下列不能判定一个四边形是平行四边形的是( )A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行另一组对边相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形6. 计算 的结果正确的是( )A、 B、 C、 D、7. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,△ABC的周长为18,AE = 3,则△ABD的周长( ) A、12 B、15 C、18 D、218. 如图,在 中,DE平分 , , ,则 ( )
A、12 B、15 C、18 D、218. 如图,在 中,DE平分 , , ,则 ( )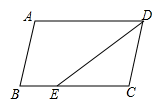 A、4 B、5 C、6 D、79. 不等式组 有3个整数解,则 的取值范围是( )
A、4 B、5 C、6 D、79. 不等式组 有3个整数解,则 的取值范围是( )
A、 B、 C、 D、10. 甲、乙两人骑自行车从相距60千米的A、B两地同时出发,相向而行,甲从A地出发至2千米时,想起有东西忘在A地,即返回去取,又立即从A地向B地行进,甲、乙两人恰好在AB中点相遇,已知甲的速度比乙的速度每小时快2.5千米,求甲、乙两人的速度,设乙的速度是x千米/小时,所列方程正确的是( )A、 B、 C、 D、二、填空题
-
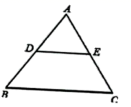
11. 在平面直角坐标系中点M(2,﹣4)关于原点对称的点的坐标为 .12. 如图,△ABC中,D、E分别是AB、AC的中点,若DE=4cm,则BC=cm.
 13. 如图,在△ABC中,AB=AC.M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为 cm2 .
13. 如图,在△ABC中,AB=AC.M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为 cm2 .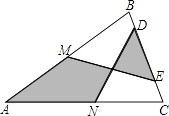 14. 当x=时,分式 的值为零.15. 把多项式 分解因式的结果是 .16. 关于x的分式方程 无解,则m的值为 .17. 已知一个多边形的内角和与外角和的比是2:1,则它的边数为 .18. 如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于 PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 .
14. 当x=时,分式 的值为零.15. 把多项式 分解因式的结果是 .16. 关于x的分式方程 无解,则m的值为 .17. 已知一个多边形的内角和与外角和的比是2:1,则它的边数为 .18. 如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于 PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 .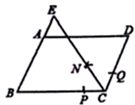
三、解答题
-
19. 解下列分式方程.(1)、 ;(2)、 .20. 先化简,再求值.1 ,其中a=﹣1.21. 解不等式组: .22. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向右平移3单位,再向上平移2个单位得到三角形A1B1C1 .
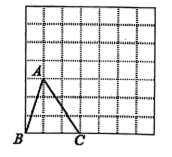 (1)、在网格中画出三角形A1B1C1 .(2)、A1B1与AB的位置关系 .23. 如图,▱ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF.
(1)、在网格中画出三角形A1B1C1 .(2)、A1B1与AB的位置关系 .23. 如图,▱ABCD的对角线AC,BD相交于点O,点E,点F在线段BD上,且DE=BF.求证:AE∥CF. 24. 在平面直角坐标系 中,直线 与直线 交于点 ,点 在直线 上.
24. 在平面直角坐标系 中,直线 与直线 交于点 ,点 在直线 上.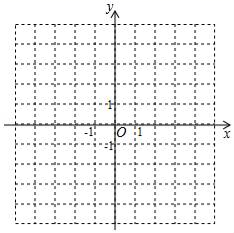 (1)、求 的值;(2)、求直线 的解析式;(3)、直接写出关于 的不等式 的解集.25. 如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,求证:BD=2EF.
(1)、求 的值;(2)、求直线 的解析式;(3)、直接写出关于 的不等式 的解集.25. 如图,已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E,F是BC的中点,求证:BD=2EF. 26. 疫情期间,为满足市民的防护需求,某医药公司想要购买A、B两种口罩.在进行市场调研时发现:A型口罩比B型口罩每件进价多了10元.用68000元购买A型口罩的件数是用32000元购买B型口罩件数的2倍.(1)、A、B型口罩进价分别为每件多少元?(2)、若该公司计划购买A、B型口罩共200件,其中A型口罩的件数不大于B型口罩的件数,且用于购买A型口罩的钱数多于购买B型口罩的钱数.设购买A型口罩x件,则符合条件的进货方案共多少种?(件数均为整数,不用列出方案)27.(1)、如图1,在△ABC中,BE平分∠ABC,CE平分∠ACD,试说明:∠E ∠A;
26. 疫情期间,为满足市民的防护需求,某医药公司想要购买A、B两种口罩.在进行市场调研时发现:A型口罩比B型口罩每件进价多了10元.用68000元购买A型口罩的件数是用32000元购买B型口罩件数的2倍.(1)、A、B型口罩进价分别为每件多少元?(2)、若该公司计划购买A、B型口罩共200件,其中A型口罩的件数不大于B型口罩的件数,且用于购买A型口罩的钱数多于购买B型口罩的钱数.设购买A型口罩x件,则符合条件的进货方案共多少种?(件数均为整数,不用列出方案)27.(1)、如图1,在△ABC中,BE平分∠ABC,CE平分∠ACD,试说明:∠E ∠A;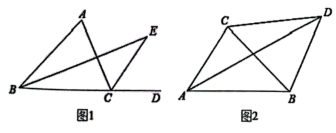 (2)、(拓展应用)如图2,在四边形ABDC中,对角线AD平分∠BAC.
(2)、(拓展应用)如图2,在四边形ABDC中,对角线AD平分∠BAC.①若∠ACD=130°,∠BCD=50°,∠CBA=40°,求∠CDA的度数;
②若∠ABD+∠CBD=180°,∠ACB=82°,写出∠CBD与∠CAD之间的数量关系.