浙江省湖州市吴兴区2021-2022学年九年级上学期期末考试数学试卷
试卷更新日期:2022-01-19 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1. 若x= ,则 =( )A、 B、6 C、 D、2. 对于二次函数y=x2 4x 1的图象,下列叙述正确的是( )A、开口向下 B、对称轴为直线x=2 C、顶点坐标为( 2, 5) D、当x≥2时,y随x增大而减小3. 如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是 ( )
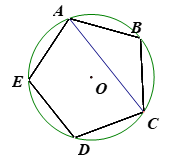 A、72° B、70° C、60° D、45°4. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( )
A、72° B、70° C、60° D、45°4. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( ) A、 B、 C、 D、5. 在二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解x的范围是( )
A、 B、 C、 D、5. 在二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解x的范围是( )x
…
1
1.1
1.2
1.3
1.4
…
y
…
1
0.49
0.04
0.59
1.16
…
A、1<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、1.3<x<1.46. 下列各选项的事件中,发生的可能性大小相等的是( )A、小明去某个路口,碰到红灯、黄灯和绿灯 B、任意抛掷一枚图钉,落地后钉尖“朝上”和“朝下” C、小亮在沿着Rt△ABC三边行走,他出现在AB,AC与BC边上 D、小红任意抛掷一枚均匀的骰子,朝上的点数为“偶数”和“奇数”7. 如图,在平面直角坐标系中,线段AB 的端点在方格线的格点上,将AB 绕点 P 顺时针方向旋转 90°,得到线段A′B′,则点 P 的坐标为( ) A、(1,2) B、(1,4) C、(0,4) D、(2,1)8. 已知一元二次方程2x2+bx 1=0的一个根是1,若二次函数y=2x2+bx 1的图象上有三个点(0,y1)、( 1,y2)、( y3),则y1 , y2 , y3的大小关系为( )A、y1<y2<y3 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y29. 如图,已知扇形OAB的半径OA=6,点P为弧AB上一动点,过点P作PC⊥OA,PD⊥OB,连结CD,当CD取得最大值时,扇形OAB的面积为( )
A、(1,2) B、(1,4) C、(0,4) D、(2,1)8. 已知一元二次方程2x2+bx 1=0的一个根是1,若二次函数y=2x2+bx 1的图象上有三个点(0,y1)、( 1,y2)、( y3),则y1 , y2 , y3的大小关系为( )A、y1<y2<y3 B、y2<y1<y3 C、y1<y3<y2 D、y3<y1<y29. 如图,已知扇形OAB的半径OA=6,点P为弧AB上一动点,过点P作PC⊥OA,PD⊥OB,连结CD,当CD取得最大值时,扇形OAB的面积为( )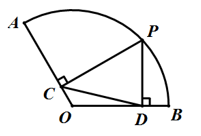 A、 B、 C、 D、10. 如图△ACB,∠ACB=90°,点O是AB的中点,CD平分∠BCO交AB于点D,作AE⊥CD分别交CO、BC于点G,E. 记△AGO的面积为S1 , △AEB的面积为S2 , 当 = 时,则 的值是( )
A、 B、 C、 D、10. 如图△ACB,∠ACB=90°,点O是AB的中点,CD平分∠BCO交AB于点D,作AE⊥CD分别交CO、BC于点G,E. 记△AGO的面积为S1 , △AEB的面积为S2 , 当 = 时,则 的值是( )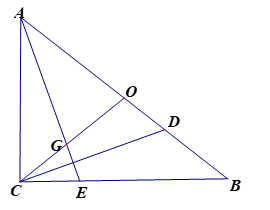 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 某同学抛掷一枚硬币,连续抛掷20次,都是反面朝上,则抛掷第21次出现正面朝上的概率是 .12. 如果将抛物线y=x2 2x向上平移,使它经过点A(0,3),那么所得新抛物线的解析式是 .13. 如图,四边形ABCD是半圆O的内接四边形,其中AB是直径,点C是弧DB的中点,若∠C=110°,则∠ABC的度数= .
 14. 如图所示的正方形网格中,每个小正方形的边长均为1,A、B、C、E、F均在格点上.若△ABC∽△DFE,则△DFE的面积是 .
14. 如图所示的正方形网格中,每个小正方形的边长均为1,A、B、C、E、F均在格点上.若△ABC∽△DFE,则△DFE的面积是 . 15. 如图,在矩形 ABCD 中,AD=3,点E是AD边上的动点,连结CE,以CE为边向右上方作正方形CEFG,过点F作 FH⊥AD,垂足为H,连结AF. 在整个变化过程中,△AEF 面积的最大值是 .
15. 如图,在矩形 ABCD 中,AD=3,点E是AD边上的动点,连结CE,以CE为边向右上方作正方形CEFG,过点F作 FH⊥AD,垂足为H,连结AF. 在整个变化过程中,△AEF 面积的最大值是 . 16. 如图,在抛物线 (a >0)上有两点P、Q,点P的坐标为(4m,y1),点Q的坐标为(m,y2)(m>0),点M在y轴上,M的坐标为(0, 1).
16. 如图,在抛物线 (a >0)上有两点P、Q,点P的坐标为(4m,y1),点Q的坐标为(m,y2)(m>0),点M在y轴上,M的坐标为(0, 1). (1)、用含a、m的代数式表示 =.(2)、连接PM,QM,小磊发现:当直线PM与直线QM关于直线y= 对称时, 为定值d,则d=.
(1)、用含a、m的代数式表示 =.(2)、连接PM,QM,小磊发现:当直线PM与直线QM关于直线y= 对称时, 为定值d,则d=.三、解答题(本题有8小题,共66分)
-
17. 2cos60° + tan45°﹣4sin30°18. 如图,在四边形ABCD中,AD∥BC,∠B=∠ACD=90°,
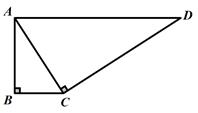 (1)、求证:△ABC∽△DCA.(2)、若BC=1,AC=2,求AD的长.19. 两人做“锤子、剪刀、布”的游戏.游戏规则是:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜.若两人出相同的手势,则认为此次游戏无效,重新开始游戏.
(1)、求证:△ABC∽△DCA.(2)、若BC=1,AC=2,求AD的长.19. 两人做“锤子、剪刀、布”的游戏.游戏规则是:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜.若两人出相同的手势,则认为此次游戏无效,重新开始游戏. (1)、请用画树状图或列表法写出游戏中所有可能出现的有效结果.(2)、在这个游戏的有效结果中,无论你出“锤子、剪刀、布”中的哪一个,你获胜的概率是多少?20. 已知二次函数 的图象过点A( 1,0),点B(3,0)和点C.(1)、若点C(0,3),求二次函数表达式;(2)、若点C(m,n),证明:当 时,总有am2+bm a+b .21. 如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.
(1)、请用画树状图或列表法写出游戏中所有可能出现的有效结果.(2)、在这个游戏的有效结果中,无论你出“锤子、剪刀、布”中的哪一个,你获胜的概率是多少?20. 已知二次函数 的图象过点A( 1,0),点B(3,0)和点C.(1)、若点C(0,3),求二次函数表达式;(2)、若点C(m,n),证明:当 时,总有am2+bm a+b .21. 如图为一种翻盖式圆柱形茶杯,底面直径为15cm,高为20cm.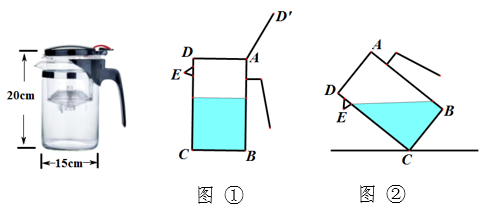 (1)、如图①,小明通过按压点A打开杯盖AD注入热水(点D,D’为对应点).若∠DAD’=120°,求点D的运动路径长.(2)、如图②,将茶杯支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出,求此时杯子最高点A距离桌面的距离.(参考数据sin53°≈0.8,cos53°≈0.6)22. 如图,已知AB是⊙O的直径,AB=6,sinC= .
(1)、如图①,小明通过按压点A打开杯盖AD注入热水(点D,D’为对应点).若∠DAD’=120°,求点D的运动路径长.(2)、如图②,将茶杯支在桌子上,当杯底倾斜到与桌面呈53°时,恰好将热水倒出,求此时杯子最高点A距离桌面的距离.(参考数据sin53°≈0.8,cos53°≈0.6)22. 如图,已知AB是⊙O的直径,AB=6,sinC= . (1)、求弦AD的长.(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.求DF的长.23. 为响应吴兴区“千里助力,精准扶贫”活动,某销售平台为青川农户销售农产品,平台销售农产品的总运营成本为4元/千克,在销售过程中要保证农户的售价不低于7元/千克,且不超过15元/千克.如图记录了某三周的销售数据,经调查分析发现,每周的农产品销售量y(千克)与售价x(元/千克)(x为正整数)近似满足如图规律的函数关系.
(1)、求弦AD的长.(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.求DF的长.23. 为响应吴兴区“千里助力,精准扶贫”活动,某销售平台为青川农户销售农产品,平台销售农产品的总运营成本为4元/千克,在销售过程中要保证农户的售价不低于7元/千克,且不超过15元/千克.如图记录了某三周的销售数据,经调查分析发现,每周的农产品销售量y(千克)与售价x(元/千克)(x为正整数)近似满足如图规律的函数关系.
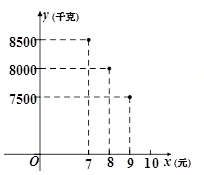 (1)、试写出y与x符合的函数表达式.(2)、若要确保农产品一周的销售量不少于6500千克,问:当农产品售价定为多少时,青川农户可获得最大收入?最大收入为多少?24. 如图,已知二次函数 的图象与x轴交于点A,B(点A在点B的左边),与y轴交于点C. 点P,Q为抛物线上两动点.
(1)、试写出y与x符合的函数表达式.(2)、若要确保农产品一周的销售量不少于6500千克,问:当农产品售价定为多少时,青川农户可获得最大收入?最大收入为多少?24. 如图,已知二次函数 的图象与x轴交于点A,B(点A在点B的左边),与y轴交于点C. 点P,Q为抛物线上两动点. (1)、若点P坐标为(1,3),求抛物线的表达式;(2)、如图①连结BC,在(1)的条件下,是否存在点Q,使得∠BCQ=∠ABC. 若存在,请求出点Q的坐标,若不存在,请说明理由;(3)、若点P为抛物线顶点,连结OP,当 a 的值从-3变化到-1的过程中,求线段OP扫过的面积.
(1)、若点P坐标为(1,3),求抛物线的表达式;(2)、如图①连结BC,在(1)的条件下,是否存在点Q,使得∠BCQ=∠ABC. 若存在,请求出点Q的坐标,若不存在,请说明理由;(3)、若点P为抛物线顶点,连结OP,当 a 的值从-3变化到-1的过程中,求线段OP扫过的面积.