广西来宾市2021-2022学年九年级上学期数学第三次月考试卷
试卷更新日期:2022-01-19 类型:月考试卷
一、选择题(共12小题,每小题3分,共36分。)
-
1. 在 中, , , ,则 的值为( )A、 B、 C、 D、2. 在Rt 中, ,若 ,则 的值为( )
 A、 B、 C、 D、3. 在Rt 中, ,则AC的长度是( )A、3cm B、4cm C、5cm D、6cm4. 已知在Rt 中, ,则 的度数是( )A、 B、 C、 D、5. 的值等于( )A、 B、 C、3 D、6. 如图所示 是 位似图形的几种画法,其中正确的个数是( )
A、 B、 C、 D、3. 在Rt 中, ,则AC的长度是( )A、3cm B、4cm C、5cm D、6cm4. 已知在Rt 中, ,则 的度数是( )A、 B、 C、 D、5. 的值等于( )A、 B、 C、3 D、6. 如图所示 是 位似图形的几种画法,其中正确的个数是( ) A、4 B、3 C、2 D、17. 如图,在 中,A,B两点在 轴上方,以点 为位似中心,在 轴的下方作 的位似图形 ,把 的边长放大到原来的2倍,设点 的对应点 的坐标是 ,则点 的坐标是( )
A、4 B、3 C、2 D、17. 如图,在 中,A,B两点在 轴上方,以点 为位似中心,在 轴的下方作 的位似图形 ,把 的边长放大到原来的2倍,设点 的对应点 的坐标是 ,则点 的坐标是( )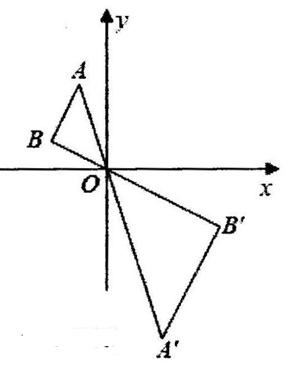 A、 B、 C、 D、8. 如图,△ABC与△DEF位似,位似中心是点O,若OC:OF=1:3,则△ABC△DEF的周长之比是( )
A、 B、 C、 D、8. 如图,△ABC与△DEF位似,位似中心是点O,若OC:OF=1:3,则△ABC△DEF的周长之比是( ) A、1:2 B、1:3 C、1:4 D、1:9. 如图,△ABC在网格(小正方形的边长均为1)中,则cos∠ABC的值是( )
A、1:2 B、1:3 C、1:4 D、1:9. 如图,△ABC在网格(小正方形的边长均为1)中,则cos∠ABC的值是( ) A、 B、 C、 D、10. 如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A、 B、 C、 D、10. 如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( ) A、 B、 C、 D、11. 某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据: ,
A、 B、 C、 D、11. 某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据: , A、6米 B、3米 C、2米 D、1米12. 如图,已知公路 上A,B两点之间的距离为20m,已知 在 的南偏西 的方向上, 在 的南偏西 方向上,则点 到公路 的距离为( )
A、6米 B、3米 C、2米 D、1米12. 如图,已知公路 上A,B两点之间的距离为20m,已知 在 的南偏西 的方向上, 在 的南偏西 方向上,则点 到公路 的距离为( ) A、10m B、 C、 D、
A、10m B、 C、 D、二、填空题(每小题3分,满分18分)
-
13. 如图,在Rt 中, 于 ,若 ,则 .
 14. 如图, 与 是位似图形,点 为位似中心,若 ,则 与 的面积比为.
14. 如图, 与 是位似图形,点 为位似中心,若 ,则 与 的面积比为.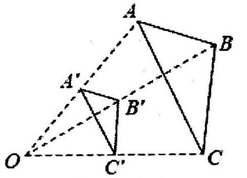 15. 已知,在 中, ,则 的面积为.16. 如图,Rt 中, 是斜边AB上的中线,已知 ,则 .
15. 已知,在 中, ,则 的面积为.16. 如图,Rt 中, 是斜边AB上的中线,已知 ,则 . 17. 如图,河坝的横断面AB的坡比是1:2,坝高BC=3米,则坡面AB的长度是米.
17. 如图,河坝的横断面AB的坡比是1:2,坝高BC=3米,则坡面AB的长度是米.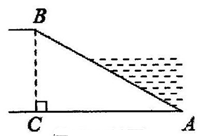 18. 如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是m.
18. 如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是m.
三、解答题(共66分)
-
19. 计算: .20. 解下列方程:(1)、 ;(2)、 (配方法).21. 如图所示是测量河宽的示意图, 与 相交于点 于点 , 于点 ,测得 ,求河宽 .
 22. 已知,一次函数 的图象与反比例函数 的图象都经过点 .(1)、求 的值及反比例函数的表达式;(2)、建立平面直角坐标系,若一次函数图象与反比例函数图象的另一个交点为 ,求 的面积.23. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),
22. 已知,一次函数 的图象与反比例函数 的图象都经过点 .(1)、求 的值及反比例函数的表达式;(2)、建立平面直角坐标系,若一次函数图象与反比例函数图象的另一个交点为 ,求 的面积.23. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).

⑴画出 绕点 顺时针旋转 后得到的 ,写出点 的坐标.
⑵以原点 为位似中心,画出将 三条边放大为原来的2倍后得 ,写出点 的坐标.
24. 如图,在 中, ,点D,E分别在AC,AB上,BD平分 , 于点 . (1)、求CD的长;(2)、求tan∠DBC的值.
(1)、求CD的长;(2)、求tan∠DBC的值.