浙江省舟山市定海五中2021-2022学年九年级上学期数学期末考前质量检测

试卷更新日期：2022-01-19 类型：期末考试

进入出卷网下载

一、选择题（10题，每小题3分，共30分）

1. 下列函数关系中，y是x的二次函数的是（）.

A、 $y = \frac{1}{x^{2}}$ B、 $y = 5 x + 3$ C、 $y = x^{2} - 3$ D、 $y = \sqrt{x^{2}}$

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、射击运动员射击一次，命中10环 B、打开电视，正在播广告 C、投掷一枚普通的骰子，掷得的点数小于10 D、在一个只装有红球的袋中摸出白球

查看试题解析
3. 如图四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转72°后，能与原图形完全重合的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在正方形网格中，格点 $△ A B C$ 绕某点顺时针旋转 $α$ 度 $(0 < α < 18 0^{°})$ ，得到格点 $Δ A_{1} B_{1} C_{1}$ ，点 $A$ 与点 $A_{1}$ ，点 $B$ 与点 $B_{1}$ ，点 $C$ 与点 $C_{1}$ 是对应点，则 $α$ 的值为( ）

A、 $5 0^{°}$ B、 $6 0^{°}$ C、 $9 0^{°}$ D、 $12 0^{°}$

查看试题解析
5. 如图，一块矩形绸布的长AB＝am，宽AD＝2m，按照图中所示的方式将它裁成相同的三面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，即 $\frac{A E}{A D} = \frac{A D}{A B}$ ，那么a的值为（）

A、 $\sqrt{6}$ B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、 $2 \sqrt{6}$

查看试题解析
6. 已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（　　）

A、有最大值 1.5，有最小值﹣2.5 B、有最大值 2，有最小值 1.5 C、有最大值 2，有最小值﹣2 5 D、有最大值 2，无最小值

查看试题解析
7. 如图，要判定 $△ A B C$ 与 $△ A E D$ 相似，欲添加一个条件，下列可行的条件有
( 1 ) $A E ： B E = A D ： D C$ ；(2) $A E ： A D = A C ： A B$ ；(3) $A D ： A C = D E ： B C$ ；(4) $∠ B E D + ∠ C = 18 0^{°}$ ；(5) $∠ B E D = ∠ C$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，将 $⊙ O$ 沿弦MN折叠，圆弧恰好经过圆心 $O$ ，点 $A$ 劣弧 $M N$ 上一点，则 $∠ M A N$ 的度数为（）

A、 $150 °$ B、 $135 °$ C、 $120 °$ D、 $105 °$

查看试题解析
9. 如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡位于点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处．点E到地面的高度ED＝3.5m，点F到地面的高度FC＝1.5m，灯泡到木板的水平距离AC＝5.4m，墙到木板的水平距离为CD＝4m．已知光在镜面反射中的入射角等于反射角，图中点A、B、C、D在同一水平面上，则灯泡到地面的高度GA为（）

A、1.2m B、1.3m C、1.4m D、1.5m

查看试题解析
10. 如图，矩形 $A B C D$ 中， $A B = 4 ， A D = 2$ ，以B为圆心，以 $B C$ 为半径画圆交边 $A B$ 于点E，点P是弧 $C E$ 上的一个动点，连结 $P D ， P A$ ，则 $\frac{1}{2} A P + D P$ 的最小值为（）

A、 $\sqrt{10}$ B、 $\sqrt{11}$ C、 $\sqrt{13}$ D、 $\sqrt{14}$

查看试题解析

二、填空题（6题，每小题4分，共24分）

11. 已知 $\frac{a - b}{2 b} = \frac{1}{3}$ ，则 $\frac{a}{b} =$ ．

查看试题解析
12. 如图，在⊙ $O$ 中，半径 $O A$ 垂直于弦 $B C$ ，点 $D$ 在圆上且 $∠ A D C = 30^{\circ}$ ，则 $∠ A O B$ 的度数为．

查看试题解析
13. 如图，已知△ADE和△ABC的相似比是1：2，且△ADE的面积是1，则四边形DBCE的面积是．

查看试题解析
14. 如图，在正方形网格中，点 $A ， B ， C ， D$ 都是小正方形的顶点， $A B$ 与 $C D$ 相交于点P，则 $s i n ∠ B P D$ 的值是.

查看试题解析
15. 如图，点C，D为线段AB的三等分点，以CD为边向上作一个正△OCD，以O为圆心，OA长为半径作弧交OC的延长线于点E，交OD的延长线于点F，若AB=6，则阴影部分的面积为．

查看试题解析
16. 如图，将二次函数 $y = x^{2} - m$ (其中 $m > 0$ )的图象在 $x$ 轴下方的部分沿 $x$ 轴翻折，图象的其余部分保持不变，形成新的图象记为 $y_{1}$ ，另有一次函数 $y = x + 2$ 的图象记为 $y_{2}$ ，若 $y_{1}$ 与 $y_{2}$ 恰有两个交点时，则 $m$ 的范围是.

查看试题解析

三、解答题（共8题；17-18每题6分，19-22每题8分，23题10分，24题12分，共66分）

17. 计算： $4 s i n 3 0^{°} c o s 6 0^{°} - t a n^{2} 3 0^{°}$ .

查看试题解析
18. 在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.

(1)、从A、D、E、F四点中任意取一点，以所取的这一点及B、C为顶点三角形，则所画三角形是等腰三角形的概率是；

(2)、从A、D、E、F四点中先后任意取两个不同的点，以所取的这两点及B、C为顶点画四边形，求所画四边形是平行四边形的概率（用树状图或列表求解）.

查看试题解析
19. 如图，AB是⊙O的直径，点F，C是⊙O上两点，且弧AF=弧FC=弧BC，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．

(1)、求证：CD是⊙O的切线；

(2)、若CD=2 $\sqrt{3}$ ，求⊙O的半径．

查看试题解析
20. 如图是由24个小正方形组成的网格图，每一个正方形的顶点都称为格点， $Δ A B C$ 的三个顶点都是格点．请按要求完成下列作图，每个小题只需作出一个符合条件的图形．

(1)、在图1网格中找格点 $D$ ，作直线 $A D$ ，使直线 $A D$ 平分 $Δ A B C$ 的面积；

(2)、在图2网格中找格点 $E$ ，作直线 $A E$ ，使直线 $A E$ 把 $Δ A B C$ 的面积分成 $1 ： 2$ 两部分．

查看试题解析
21. 二次函数y₁＝ax²+2x过点A（﹣2，0）和点B，过点A，B作一次函数y₂＝kx+b，若点B的横坐标为1．

(1)、求出二次函数与一次函数的解析式；

(2)、根据图象，当y₂＞y₁时，请直接写出x的取值范围；

(3)、若P点在抛物线y₁上，且横坐标为﹣1，求△ABP的面积．

查看试题解析
22. 摇椅是老年人很好的休闲工具，右图是一张摇椅放在客厅的侧面示意图，摇椅静止时，以O为圆心OA为半径的弧AB的中点P着地，地面NP与弧AB相切，已知∠AOB=60°，半径OA=60cm，靠背CD与OA的夹角∠ACD=127°，C为OA的中点，CD=80cm，当摇椅沿弧AB滚动至点A着地时是摇椅向后的最大安全角度．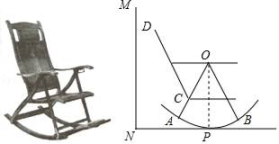

（精确到1cm，参考数据π取3.14，sin37°=0.60，cos37°=0.80，tan37°=0.75，sin67°=0.92，cos67°=0.39，tan67°=2.36， $\sqrt{2}$ =1.41， $\sqrt{3}$ =1.73）

(1)、静止时靠背CD的最高点D离地面多高？

(2)、静止时着地点P至少离墙壁MN的水平距离是多少时？才能使摇椅向后至最大安全角度时点D不与墙壁MN相碰．

查看试题解析
23. 随州某药店经销甲、乙两种口罩，若甲种口罩每包利润10元，乙种口罩每包利润20元，则每周能卖出甲种口罩40包，乙种口罩20包.突如其来的新冠病毒严重影响人们生活，口罩成为人们防疫的必须品，为了解决人们所需，药店决定把甲、乙两种口罩的零售单价都降价x元，回报顾客.经调查，甲、乙两种口罩零售单价分别每降1元，这两种口罩每周可各多销售10包.

(1)、直接写出甲、乙两种口罩每周的销售量 $y_{甲}$ ， $y_{乙}$ （包）与降价x（元）之间的函数关系式；

(2)、药店每周销售甲、乙两种口罩获得的总利润为W（元）；
①如果每周甲种口罩的销售量不低于乙种口罩的销售量的 $\frac{4}{3}$ ，求W的最大值；

②若每周总利润W（元）不低于1340元，求x的范围.

查看试题解析
24. 如图，点F在四边形ABCD的边AB上，

(1)、如图①，当四边形ABCD是正方形时，过点B作BE⊥CF，垂足为O，交AD于点E．求证：BE＝CF；

(2)、当四边形ABCD是矩形，AD＝6，AB＝8时，
①如图②，点P是BC上的一点，过点P作PE⊥CF，垂足为O，点O恰好落在对角线BD上，求 $\frac{O C}{O E}$ 的值；

②如图③，点P是BC上的一点，过点P作PE⊥CF，垂足为O，点O恰好落在对角线BD上，延长EP、AB交于点G，当BG＝2时，DE＝ ▲ ．

查看试题解析