辽宁省沈阳市于洪区2021年中考数学二模试卷

试卷更新日期：2022-01-19 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣5的相反数是（）

A、﹣5 B、5 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 某几何体的三视图如图所示，这个几何体是（）

A、三棱柱 B、球体 C、圆锥体 D、圆柱体

查看试题解析
3. 如图， $l_{1} / / l_{2}$ ， $A E ⊥ B E$ .若 $∠ 1 = 130 °$ ，则∠2的度数为（）

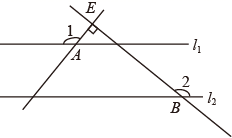A、120° B、130° C、140° D、150°

查看试题解析
4. 在平面直角坐标系中，将点 $M (3 ， 1)$ 先向上平移2个单位长度，再向右平移3个单位长度，则移动后的点的坐标是（）

A、 $(5 ， 4)$ B、 $(6 ， 3)$ C、 $(0 ， 3)$ D、 $(0 ， - 1)$

查看试题解析
5. 若 $m^{2} + 2 m = 1$ ，则 $4 m^{2} + 8 m - 3$ 的值是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 若反比例函数 $y = \frac{k - 1}{x}$ 的图象位于第二、四象限，则k的取值范围是（）

A、 $k \leq 1$ B、 $k < 1$ C、 $k > 1$ D、 $k < 0$

查看试题解析
7. 关于“可能性是1%的事件在100次试验中发生的次数”，下列说法错误的是（）

A、可能一次也不发生 B、可能发生一次 C、可能发生两次 D、一定发生一次

查看试题解析
8. 某种服装，平均每天可销售50件，每件利润40元．若每件降价5元，则每天多售10件．如果要在扩大销量的同时，使每天的总利润达到2100元，每件应降价多少元？若设每件应降价 $x$ 元，则可列方程得（）

A、 $(40 - x) (50 + 10 \times \frac{x}{5}) = 2100$ B、 $(40 - x) (50 - 10 \times \frac{x}{5}) = 2100$ C、 $(40 + x) (50 - 10 \times \frac{x}{5}) = 2100$ D、 $(40 + x) (50 + 10 \times \frac{x}{5}) = 2100$

查看试题解析
9. 如图，在半径为5的⊙O中，弦AB=6，点C是优弧 $\overset{⌢}{A B}$ 上一点（不与A，B重合），则cosC的值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，对称轴为直线 $x = 1$ ，与 $x$ 轴的一个交点为 $(3 ， 0)$ .下列结论① $b^{2} - 4 a c < 0$ ；② $4 a + 2 b + c > 0$ ；③图象与 $x$ 轴的另一个交点为 $(- 1 ， 0)$ ；④当 $x > 0$ 时， $y$ 随 $x$ 的增大而减小，所有正确结论的序号是（）

A、①③ B、①④ C、②③ D、②④

查看试题解析

二、填空题

11. 因式分解： $6 a b - a^{2} - 9 b^{2} =$ .

查看试题解析
12. 甲、乙两块水稻田，随机测量若干株水稻的高度后，计算方差分别为 $s_{甲}^{2} = 18.5$ ， $s_{乙}^{2} = 30.2$ ，则两块水稻田稻苗高度比较均匀的是.（填“甲”或“乙”）

查看试题解析
13. 化简： $(\frac{2}{a - 2} - \frac{1}{a}) \div \frac{a + 2}{a} =$ .

查看试题解析
14. 甲、乙两人分别从A、B两地出发，相向而行．图中的 $l_{1}$ ， $l_{2}$ 分别表示甲、乙离B地的距离 $y (km)$ 与甲出发后所用时间 $x (h)$ 的函数关系图象，则甲出发小时与乙相遇．

查看试题解析
15. 如图，要在夹角为30°的两条小路 $O A$ 与 $O B$ 形成的角状空地上建一个三角形花坛，分别在边 $O A$ 和 $O B$ 上取点 $P$ 和点 $Q$ ，并扎起篱笆将花坛保护起来（篱笆的厚度忽略不计）.若 $O P$ 和 $O Q$ 两段篱笆的总长为8米，则当 $O P =$ 米时，该花坛 $P O Q$ 的面积最大.

查看试题解析
16. 如图，在正方形 $A B C D$ 外侧作直线 $D E$ ，点 $C$ 关于直线 $D E$ 的对称点为 $M$ ，连接 $C M$ ， $A M$ .其中 $A M$ 交直线 $D E$ 于点 $N$ .若 $45 ° < ∠ C D E < 90 °$ ，则当 $M N = 4$ ， $A N = 3$ 时，正方形 $A B C D$ 的边长为.

查看试题解析

三、解答题

17. 计算： $| 2 - \sqrt{8} | + (- 3)^{0} - 6 c o s 45 ° + {(- \frac{1}{4})}^{- 1}$ .

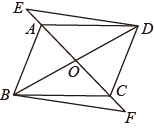
查看试题解析
18. 某学校开展“垃圾分类，从我做起”的宣讲活动，该活动的宣讲员从甲、乙、丙、丁四名学生中随机抽选.

(1)、若只抽选一名学生，乙被选中的概率为.

(2)、若随机抽选两名学生，请用列表法或画树状图法求乙被选中的概率.

查看试题解析
19. 如图，在 $▱ A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，点 $E$ ， $F$ 分别在 $C A$ 和 $A C$ 的延长线上，且 $A E = C F$ ，连接 $D E$ ， $B F$ .求证： $D E = B F$ .

查看试题解析
20. 某中学为了解学生参加户外活动的情况，对全校学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如下两幅不完整的统计图表.根据统计图表提供的信息，解答下列问题：
户外活动时间的统计表
组别
时间/小时
人数
$A$
$0.5 \leq x < 1$
8
$B$
$1 \leq x < 1.5$
14
$C$
$1.5 \leq x < 2$
$m$
$D$
$2 \leq x < 2.5$
$n$
$E$
$2.5 \leq x < 3$
3

(1)、本次被调查的学生有人；

(2)、在扇形统计图中，组别D所在扇形的圆心角度数是°；

(3)、被调查的学生每天户外活动时间的中位数出现在组；

(4)、若该校共有800名学生，根据抽样调查的结果，请估计该校有多少名学生每天户外活动时间不少于2小时.

查看试题解析
21. 某店主购进 $A$ ， $B$ 两种礼盒.已知 $A$ ， $B$ 两种礼盒的单价比为2∶3，单价和为10元.该店主进 $B$ 种礼盒的数量是 $A$ 种礼盒数量的2倍少1个，且这两种礼盒花费不超过398元，则 $A$ 种礼盒最多购买多少个？

查看试题解析
22. 如图， $B O$ 是 $△ A B C$ 的角平分线，以点 $O$ 为圆心， $O C$ 为半径作 $⊙ O$ 交 $A C$ 于点 $D$ .当 $B C$ 为 $⊙ O$ 切线时.

(1)、求证： $A B$ 是 $⊙ O$ 的切线；

(2)、若 $s i n A = \frac{1}{2}$ ， $A D = 3$ ，求图中阴影部分面积.（结果保留 $π$ 和根号）

查看试题解析
23. 在平面直角坐标系中，点 $A (0 ， 3)$ ，直线 $A B / / x$ 轴.在矩形 $O C D E$ 中， $O C = 4$ ， $O E = 3$ .以点 $C$ 在第一象限内直线 $A B$ 上时为初始位置，将矩形 $O C D E$ 以点 $O$ 为中心逆时针旋转，旋转角为 $α$ .直线 $O C$ ，直线 $D E$ 分别与直线 $A B$ 相交于点 $M$ ， $N$ .

(1)、如图1，当顶点 $D$ 落在直线 $A B$ 上时（此时点 $N$ 与点 $D$ 重合）.
①求证： $△ M A O ≌ △ M C D$ ；
②求点 $M$ 的横坐标；

(2)、如图2，当顶点 $D$ 落在 $y$ 轴正半轴上时，请直接写出点 $M$ 的横坐标；

(3)、在矩形 $O C D E$ 旋转过程中，当 $0 ° < α < 90 °$ 时，若 $A N = 3 A M$ ，请直接写出此时点 $M$ 的横坐标.

查看试题解析
24. 在菱形 $A B C D$ 中， $∠ B = 60 °$ .点 $E$ ， $F$ 分别在边 $B C$ ， $C D$ 上，且 $B E = C F$ .连接 $A E$ ， $A F$ .

(1)、如图1，连接 $E F$ ，求证： $△ A E F$ 是等边三角形；

(2)、 $A G$ 平分 $∠ E A F$ 交 $B C$ 于点 $G$ .
①如图2， $A G$ 交 $E F$ 于点 $M$ ，点 $N$ 是 $B C$ 的中点，当 $B E = 4$ 时，求 $M N$ 的长.
②如图3， $O$ 是 $A C$ 的中点，点 $H$ 是线段 $A G$ 上一动点（点 $H$ 与点 $A$ ，点 $G$ 不重合）.当 $A B = 12$ ， $B E = 4$ 时，是否存在直线 $O H$ 将 $△ A C E$ 分成三角形和四边形两部分，其中三角形的面积与四边形的面积比为1∶3.若存在，请直接写出 $\frac{A H}{A G}$ 的值；若不存在，请说明理由.

查看试题解析
25. 在平面直角坐标系中，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 与 $x$ 轴交于点 $A (- 2 ， 0)$ 和点 $B$ （点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C (0 ， 3)$ .

(1)、求抛物线的表达式；

(2)、如图，点 $D$ 是第一象限抛物线上一点，过 $D$ 作 $D M ⊥ x$ 轴于点 $M$ ，交 $B C$ 于点 $N$ .若点 $N$ 为 $D M$ 中点，求点 $D$ 的坐标，并直接写出此时直线 $D C$ 的表达式.

(3)、在（2）的条件下，点 $E$ 为 $y$ 轴右侧抛物线上一点，过点 $E$ 作直线 $D C$ 的垂线，垂足为 $P$ ，若 $∠ E C P = ∠ D A B$ ，请直接写出点 $E$ 的坐标.

查看试题解析

组别	时间/小时	人数
$A$	$0.5 \leq x < 1$	8
$B$	$1 \leq x < 1.5$	14
$C$	$1.5 \leq x < 2$	$m$
$D$	$2 \leq x < 2.5$	$n$
$E$	$2.5 \leq x < 3$	3