湖北省襄阳市谷城县2021年九年级下学期中考适应性考试数学试卷
试卷更新日期:2022-01-19 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 一把直尺和一块含30°角的直角三角板ABC如图所示摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )
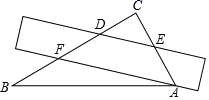 A、5° B、15° C、25° D、35°3. 下列计算正确的是( )A、 B、 C、 D、4. 南宁到玉林城际铁路投资约278亿元,将数据278亿用科学记数法表示是( )A、278×108 B、27.8×109 C、2.78×1010 D、2.78×1085. 下列图形既是轴对称图形又是中心对称图形的是( )A、
A、5° B、15° C、25° D、35°3. 下列计算正确的是( )A、 B、 C、 D、4. 南宁到玉林城际铁路投资约278亿元,将数据278亿用科学记数法表示是( )A、278×108 B、27.8×109 C、2.78×1010 D、2.78×1085. 下列图形既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图是由5个大小相同的小正方体摆成的几何体,它的俯视图是( )
6. 如图是由5个大小相同的小正方体摆成的几何体,它的俯视图是( ) A、
A、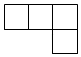 B、
B、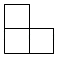 C、
C、 D、
D、 7. 不等式组 的解集在数轴上表示正确的是( )A、
7. 不等式组 的解集在数轴上表示正确的是( )A、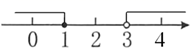 B、
B、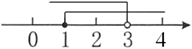 C、
C、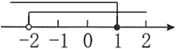 D、
D、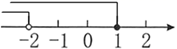 8. 下列说法正确的是( )A、明天的降水概率为80%,则明天80%的时间下雨,20%的时间不下雨 B、抛掷一枚质地均匀的硬币两次,必有一次正面朝上 C、了解一批花炮的燃放质量,应采用抽样调查方式 D、一组数据的众数一定只有一个9. 《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为 ,买鸡的钱数为 ,可列方程组为( )A、 B、 C、 D、10. 如图,四边形 是菱形, 经过点 、 、 ,与 相交于点 ,连接 、 .若 ,则 的度数为( )
8. 下列说法正确的是( )A、明天的降水概率为80%,则明天80%的时间下雨,20%的时间不下雨 B、抛掷一枚质地均匀的硬币两次,必有一次正面朝上 C、了解一批花炮的燃放质量,应采用抽样调查方式 D、一组数据的众数一定只有一个9. 《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为 ,买鸡的钱数为 ,可列方程组为( )A、 B、 C、 D、10. 如图,四边形 是菱形, 经过点 、 、 ,与 相交于点 ,连接 、 .若 ,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
11. 分式方程:的解是.12. 先化简,再求值: ,其中 .13. 某校为了解九年级学生每天参加体育锻炼额时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):
30 60 70 10 30 115 70 60 75 90 15 70 40 75 105 80 60 30 70 45
对以上数据进行整理分析,得到下列表一和表二:
表一
时间t(单位:分钟)
人数
2
a
10
b
表二
平均数
中位数
众数
60
c
d
根据以上提供信息,解答下列问题:
(1)、填空①a= b=
②c= d=
(2)、如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数。14. 美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得 , .若米,求观景亭D到南滨河路AC的距离(参考数据: , , )(结果保留整数). 15. 如图,AD是△ABC的角平分线
15. 如图,AD是△ABC的角平分线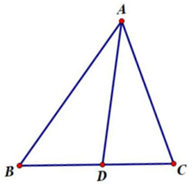 (1)、作线段AD的垂直平分线EF,分别交AB、AC于点E、F;
(1)、作线段AD的垂直平分线EF,分别交AB、AC于点E、F;(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)
(2)、连接DE、DF,四边形AEDF是形.(直接写出答案)16. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究函数的图象与性质,探究过程如下: (1)、写出自变量x的取值范围;(2)、画函数图象;
(1)、写出自变量x的取值范围;(2)、画函数图象;列表:下表是x与y的几组对应值,其中 ▲ ;
x
…
-3
-2
-1
1
2
3
…
y
…
1
2
4
4
2
m
…
描点画图:利用所给的网格,建立平面直角坐标系,描出表中各对对应值为坐标的点,画出该函数图象;
(3)、通过观察图象,写出该函数的两条性质:①;
②.
17. 如图,在 中, , 是斜边 上的中线,以 为直径的 分别交 、 于点 、 ,过点 作 ,垂足为 . (1)、若 的半径为 , ,求 的长;(2)、求证: 与 相切.18. 某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.
(1)、若 的半径为 , ,求 的长;(2)、求证: 与 相切.18. 某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.行李的重量xkg
快递费
不超过1kg
10元
超过1kg但不超过5kg的部分
3元/kg
超过5kg但不超过15kg的部分
5元/kg
 (1)、如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?(2)、如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;(3)、某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?19. 问题背景:如图(1),已知 , 求证:;
(1)、如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?(2)、如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;(3)、某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?19. 问题背景:如图(1),已知 , 求证:;尝试应用:如图(2),在和中, , , 与相交于点.点在边上, , 求的值;
拓展创新:如图(3),是内一点, , , , , 直接写出的长.


 20. 在平面直角坐标系中,已知抛物线和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.(1)、若抛物线C与直线l有交点,求a的取值范围;(2)、当a=-1,二次函数的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;(3)、若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
20. 在平面直角坐标系中,已知抛物线和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.(1)、若抛物线C与直线l有交点,求a的取值范围;(2)、当a=-1,二次函数的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;(3)、若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.三、填空题