陕西省高陵区2021-2022学年八年级上学期阶段测试数学试卷(二)
试卷更新日期:2022-01-19 类型:月考试卷
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 二元一次方程的解可以是( )A、 B、 C、 D、3. 如图,在坐标系中用手盖住一点P,若点P到x轴的距离为2,到y轴的距离为6,则P点的坐标是( )
 A、 B、 C、 D、4. 已知二元一次方程组则( )A、6 B、4 C、3 D、25. 下列四个选项中,不符合直线的性质与特征的是( )A、经过第一、三、四象限 B、y随x的增大而增大 C、与x轴交于点 D、与y轴交于点6. 实数a,b在数轴上的位置如图所示,则( )
A、 B、 C、 D、4. 已知二元一次方程组则( )A、6 B、4 C、3 D、25. 下列四个选项中,不符合直线的性质与特征的是( )A、经过第一、三、四象限 B、y随x的增大而增大 C、与x轴交于点 D、与y轴交于点6. 实数a,b在数轴上的位置如图所示,则( ) A、 B、 C、 D、7. 小强每天坚持做引体向上的锻炼,下表是他记录的某一周每天做引体向上的个数.
A、 B、 C、 D、7. 小强每天坚持做引体向上的锻炼,下表是他记录的某一周每天做引体向上的个数.星期
日
一
二
三
四
五
六
个数
11
12
10
13
13
13
12
对于小强做引体向上的个数,下列说法错误的是( )
A、平均数是12 B、众数是13 C、中位数是12.5 D、方差是8. 如图,9个大小、形状完全相同的小长方形,组成了一个周长为46的大长方形 , 若设小长方形的长为x,宽为y,则可列方程为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
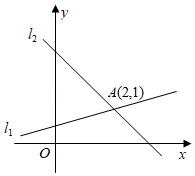
9. 若2x﹣y=12,用含有x的代数式表示y,则y=.10. 在平面直角坐标系中,点A与点关于x轴对称,那么点A的坐标为.11. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .
 12. 某学校八年级(2)班有20名学生参加学校举行的“学党史、看红书”知识竞赛,成绩统计如图.这个班参赛学生的平均成绩是 .
12. 某学校八年级(2)班有20名学生参加学校举行的“学党史、看红书”知识竞赛,成绩统计如图.这个班参赛学生的平均成绩是 .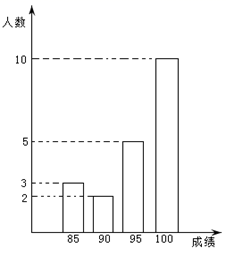 13. 如图,在中, , , , D为边上一点,将沿折叠,若点B恰好落在线段的延长线上的点E处,则的长为.
13. 如图,在中, , , , D为边上一点,将沿折叠,若点B恰好落在线段的延长线上的点E处,则的长为.
三、解答题
-
14. 计算:.15. 用代入法解方程组:16. 用加减法解方程组:17. 已知 , , 求的值.18. 已知一组数据:0,1,-3,6,a,4.其唯一众数为4,求这组数据的中位数.19. 如图,在平面直角坐标系中,的三个顶点坐标为 , , , 在图中作出关于y轴对称的图形 , 并写出D,E,F的坐标.
 20. 如图,Rt△ABC中的顶点A,C分别在平面直角坐标系的x轴,y轴上,且∠ACB=90°,AC=8,BC=4.当OA=OC时,求四边形OABC的面积.
20. 如图,Rt△ABC中的顶点A,C分别在平面直角坐标系的x轴,y轴上,且∠ACB=90°,AC=8,BC=4.当OA=OC时,求四边形OABC的面积. 21. 如图,过点的直线:与直线:交于点.求k,b,m的值.
21. 如图,过点的直线:与直线:交于点.求k,b,m的值. 22. 已知关于x,y的方程组 , 若该方程组的解x,y的值互为相反数,求a的值和方程组的解.23. 中药是我国的传统医药,其独特的疗效体现了我们祖先的智慧,并且在抗击新冠疫情中,中医药发挥了重要的作用.现某中药材种植基地欲将一批150吨的重要中药材运往某药品生产厂,现有甲、乙两种车型供运输选择,每辆车的运载能力(假设每辆车均满载)和运费如下表所示:
22. 已知关于x,y的方程组 , 若该方程组的解x,y的值互为相反数,求a的值和方程组的解.23. 中药是我国的传统医药,其独特的疗效体现了我们祖先的智慧,并且在抗击新冠疫情中,中医药发挥了重要的作用.现某中药材种植基地欲将一批150吨的重要中药材运往某药品生产厂,现有甲、乙两种车型供运输选择,每辆车的运载能力(假设每辆车均满载)和运费如下表所示:车型
甲
乙
运载量(吨/辆)
10
12
运费(元/辆)
700
720
若全部中药材用甲、乙两种车型一次性运完,需支付运费9900元,问甲、乙两种车型各需多少辆?
24. 问题
情境:在平面直角坐标系中有两个不重合的点,分别为点和点.若 , , 则线段轴,且线段的长度为;若 , , 则线段轴,且线段的长度为.(1)、应用
若点P,Q的坐标分别为 , , 则线段∥轴,的长度为.(2)、若点 , 且线段轴, , 则点D的坐标为.(3)、拓展
我们规定:在平面直角坐标系中,若 , , 则式子的值就叫做线段的“勾股距”,记作 , 即.例如:有点与点 , 则线段的勾股距为.解决下列问题:
①已知 , 若 , 则 .
②已知 , , 若 , 求t的值.
25. 甲、乙、丙三名候选人要参加学校学生会干部竞选,按程序分别进行答辩、笔试和民主投票.答辩、笔试成绩如下表所示,学生民主投票每张选票只限填写甲、乙、丙中的一人,且每张选票记1分.统计得票后,绘出如下所示不完整的统计图.答辩、笔试成绩统计表
人员
甲
乙
丙
答辩成绩(分)
95
88
86
笔试成绩(分)
80
86
90

根据以上信息,请解答下列问题.
(1)、参加投票的共有人,乙的得票率是.(2)、补全条形统计图.(3)、学校将答辩、笔试和学生投票三项得分按4:4:2的比例确定每位候选人的总成绩,总成绩最高者当选,试通过计算说明哪位候选人当选.26. 如图,直线:与x轴交于点A,与y轴交于点B,直线:与x轴交于点 , 与y轴交于点 , 直线 , 交于点E. (1)、求直线的函数表达式.(2)、试说明.(3)、若P为直线上一点,当时,求点P的坐标.
(1)、求直线的函数表达式.(2)、试说明.(3)、若P为直线上一点,当时,求点P的坐标.