湖北省咸宁市崇阳县2021-2022学年九年级上学期12月月考数学试卷

试卷更新日期：2022-01-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（　　）

A、3x+1＝0 B、x²﹣3＝0 C、y+x²＝4 D、 $\frac{1}{x}$ +x²＝2

查看试题解析
2. 下列防控疫情的图标中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点 $A (- 2 ， 1)$ 与点 $B$ 关于原点对称，则点 $B$ 的坐标为（）．

A、 $(- 2 ， 1)$ B、 $(2 ， - 1)$ C、 $(2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
4. 将抛物线y＝x²向左平移3个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（）

A、y＝（x＋3）²＋3 B、y＝（x﹣3）²＋1 C、y＝（x＋2）²＋1 D、y＝（x＋3）²＋1

查看试题解析
5. 某商品原价289元，经连续两次降价后售价为256元，设平均每降价的百分率为x，则下面所列方程正确的是（　　）

A、289（1﹣x）²=256 B、256（1﹣x）²=289 C、289（1﹣2x）²=256 D、256（1﹣2x）²=289

查看试题解析
6. 若圆锥的底面半径为2cm，侧面展开图的面积为6πcm² ，则圆锥的母线长为（）

A、1cm B、2cm C、3cm D、 $\frac{π}{2}$ cm

查看试题解析
7. 如图，在⊙O中， $\overset{⌢}{A B} = \overset{⌢}{A C}$ ， $∠ B A C = 70 °$ ，则 $∠ A E C$ 的度数是（）

A、 $65 °$ B、 $75 °$ C、 $50 °$ D、 $55 °$

查看试题解析
8. 点P₁（﹣1，y₁），P₂（3，y₂），P₃（5，y₃）均在二次函数y＝﹣x²+2x+c的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＝y₂＞y₃ B、y₁＞y₂＞y₃ C、y₃＞y₂＞y₁ D、y₃＞y₁＝y₂

查看试题解析
9. 如图，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED，若BC＝8，BD＝6，则△AED的周长是（）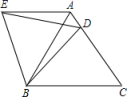

A、10 B、12 C、14 D、15

查看试题解析
10. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若AE＝6，AB＝5，则BF的长为（）

A、5 B、6 C、8 D、12

查看试题解析

二、填空题

11. 若关于x的函数y＝（1﹣a）x²﹣x是二次函数，则a的取值范围是

查看试题解析
12. 已知关于x的一元二次方程 $x^{2} + x + m = 0$ 的一个根是x=1，那么这个方程的另一个根是．

查看试题解析
13. 以 $40 m / s$ 的速度将小球沿与地面成 $30$ 度角的方向击出时，球的飞行路线是一条抛物线.如果不考虑空气阻力，球的飞行高度h（单位m）与飞行时间t（单位s）之间具有函数关系： $h = 20 t - 5 t^{2}$ ，那么球从飞出到落地要用的时间是.

查看试题解析
14. 已知关于x的二次函数y＝﹣（x﹣5）²＋1，当1≤x≤4时，函数的最大值为．

查看试题解析
15. 二次函数y=kx²-4x+2的图象与x轴有公共点，则k取值范围是

查看试题解析
16. 如图，⊙O的半径OA＝5，B是⊙O上的动点（不与点A重合），过点B作⊙O的切线BC，BC＝OA，连接OC，AC．当△OAC是直角三角形时，其斜边为．

查看试题解析

三、解答题

17.

(1)、（x﹣1）²＝2（x﹣1）

(2)、2x²﹣5x﹣2＝0

查看试题解析
18. 如图，在平面直角坐标系中△ABC的三个顶点的坐标分别为A（5，4），B（0，3），C（2，1）．

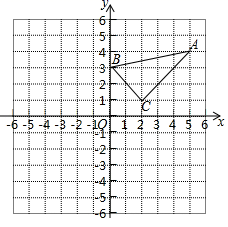
⑴画出△ABC关于原点成中心对称的△A₁B₁C₁ ，并写出点C₁的坐标；

⑵画出将△A₁B₁C₁绕点C₁按顺时针方向旋转90°所得的△A₂B₂C₁ ，并写出点A₂坐标．

查看试题解析
19. 如图，AB是⊙O的弦，C、D为直线AB上两点，OC＝OD，求证：AC＝BD.

查看试题解析
20. 一个不透明的袋子中装有四个小球，球面上分别标有数字-1，0，1，2四个数字．这些小球除了数字不同外，其他都完全相同，袋内小球充分搅匀．

(1)、随机地从袋中摸出一个小球，则摸出标有数字2的小球的概率为；

(2)、小强设计了如下游戏规则：先从袋中随机摸出一个小球（不放回），然后再从余下的三个小球中随机摸出一个小球．把2次摸到的小球数字相加，和为奇数，甲获胜；和为偶数，乙获胜．小强设计的游戏规则公平吗？为什么？（请用画树状图或列表说明理由）

查看试题解析
21. 如图，利用函数y＝x²﹣4x＋3的图象，直接回答：

(1)、方程x²﹣4x＋3＝0的解是；

(2)、当x满足时，y随x的增大而增大；

(3)、当x满足时，函数值大于0；

(4)、当0＜x＜5时，y的取值范围是．

查看试题解析
22. 如图，直线AB经过⊙O上的点C，直线BO与⊙O交于点F和点D，OA与⊙O交于点E，与DC交于点G，OA＝OB，CA＝CB．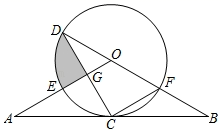

(1)、求证：AB是⊙O的切线；

(2)、若FC∥OA，CD＝6，求图中阴影部分面积．

查看试题解析
23. 某大学生创业团队抓住商机，购进一批干果分装成营养搭配合理的小包装后出售，每袋成本3元.试销期间发现每天的销售量y（袋）与销售单价x（元）之间满足一次函数关系，部分数据如表所示，其中3.5≤x≤5.5，另外每天还需支付其他费用80元.

销售单价 $x$ （元）

3.5

5.5

销售量 $y$ （袋）

280

120

(1)、请直接写出y与x之间的函数关系式；

(2)、如果每天获得160元的利润，销售单价为多少元？

(3)、设每天的利润为w元，当销售单价定为多少元时，每天的利润最大？最大利润是多少元？

查看试题解析
24. △ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．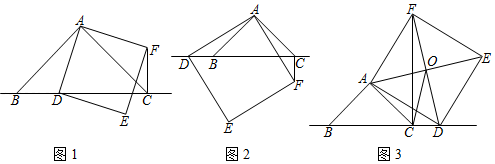

(1)、探究猜想，如图1，当点D在线段BC上时，
①BC与CF的位置关系为；

②BC、CD、CF之间的数量关系为；

(2)、深入思考，如图2，当点D在线段CB的延长线上时，结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

(3)、拓展延伸，如图3，当点D在线段BC的延长线上时，正方形ADEF对角线交于点O．若已知AB＝4 $\sqrt{2}$ ， CD＝ $\frac{1}{4}$ BC，请求出OC的长．

查看试题解析
25. 抛物线y＝mx²﹣2mx﹣3m与x轴交于A，B两点，点A在点B的左侧．交y轴于点C，

(1)、直接写出：抛物线的对称轴；，点A的坐标为，点B的坐标为；

(2)、若点C的坐标为（0，－3），在此条件下求下列问题：
①在下面的直角坐标系中，画出函数图象；

②当n≤x≤3时，函数值y的取值范围为﹣4≤y≤0，直接写出n的取值范围；

③点C关于x轴的对称点为点D，若过点D的直线y＝kx＋b与抛物线在x轴下方（不含x轴上的点）的部分无公共点，结合图象，求出k的取值范围．

查看试题解析

销售单价 $x$ （元）	3.5	5.5
销售量 $y$ （袋）	280	120