湖北省天门市六校平行班2021-2022学年九年级上学期12月联考数学试卷

试卷更新日期：2022-01-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 若关于 $x$ 的一元二次方程 $x^{2} - a x + 6 = 0$ 的一个根是2，则 $a$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 下列图形既是中心对称又是轴对称的是（）

A、 B、 C、 D、

查看试题解析
3. 下列事件中，是随机事件的是（）

A、三角形中任意两边之和大于第三边 B、太阳从东方升起 C、车辆随机到达一个路口，遇到绿灯 D、一个有理数的绝对值为负数

查看试题解析
4. 如图，电路图上有四个开关A，B，C，D和一个小灯泡，闭合开关D或同时闭合开关A，B，C，都可使小灯泡发光.任意闭合其中一个开关，则小灯泡发光的概率等于（）.

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
5. 如图， $⊙ O$ 中，弦 $A B ， C D$ 相交于点 $P ， ∠ A = 40 ° ， ∠ A P D = 75 °$ ，则 $∠ B =$ （）.

A、 $15 °$ B、 $40 °$ C、 $75 °$ D、 $35 °$

查看试题解析
6. 在平面直角坐标系中，将抛物线 $y = 2 {(x - 1)}^{2} + 3$ 先向左平移2个单位，再向下平移1个单位，得到的抛物线解析式为（）

A、 $y = 2 {(x + 1)}^{2} + 2$ B、 $y = 2 {(x - 3)}^{2} + 2$ C、 $y = 2 {(x + 1)}^{2} + 4$ D、 $y = 2 {(x - 3)}^{2} + 4$

查看试题解析
7. 已知圆的半径为10cm，如果圆心O到直线的距离为12cm，那么这条直线和这个圆的位置关系是（）

A、相离 B、相切 C、相交 D、都可能

查看试题解析
8. 已知圆锥的底面圆半径为3cm，母线长为5cm，则这个圆锥的侧面积是（）

A、15π cm² B、15 cm² C、30π cm² D、30 cm²

查看试题解析
9. 如果关于x的一元二次方程ax²+x﹣1=0有实数根，则a的取值范围是（）

A、a＞﹣ $\frac{1}{4}$ B、a≥﹣ $\frac{1}{4}$ C、a≥﹣ $\frac{1}{4}$ 且a≠0 D、a＞ $\frac{1}{4}$ 且a≠0

查看试题解析
10. 二次函数y=ax²+bx+c的图象如图所示，对称轴是x=－1．有以下结论：①abc>0，②4ac＜b² ， ③2a+b=0，④a－b+c>2，其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 若点 $P (m ， 5)$ 与点 $P' (3 ， n)$ 关于原点成中心对称，则 $m + n =$ .

查看试题解析
12. 将二次函数 $y = x^{2} - 4 x + 5$ 化为 $y = {(x - h)}^{2} + k$ 的形式，则 $y =$ ．

查看试题解析
13. 一个不透明的袋子中装 $8$ 个小球，其中 $3$ 个红球， $3$ 个白球， $2$ 个黑球，小球出颜色外形状、大小完全相同．现从中随机摸出一个小球，摸出的小球是红色的概率为．

查看试题解析
14. 某小组有若干人，新年大家互相发一条微信视福，已知全组共发微信56条，则这个小组的人数为人.

查看试题解析
15. 如图，在 $⊙ O$ 中， $O A = 3$ ， $∠ C = 45 °$ ，则图中阴影部分的面积是.（结果保留 $π$ ）

查看试题解析
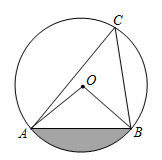16. 如图，在△ABC中，AB=AC=4，将△ABC绕点A顺时针旋转30°，得到△ACD，延长AD交BC的延长线于点E，则DE的长为

查看试题解析

三、解答题

17. 解下列方程：

(1)、x²+4x﹣5＝0

(2)、（x﹣3）²＝2（3﹣x）

查看试题解析
18. 已知关于x的一元二次方程 ${(x - m)}^{2} - 2 (x - m) = 0$ (m为常数)．

(1)、求证：不论m为何值，该方程总有两个不相等的实数根；

(2)、若该方程一个根为3，求m的值．

查看试题解析
19. 小明和小亮进行“转盘”游戏：下面是两个可以自由转动的转盘，游戏者同时转动两个转盘，如果两个转盘转出的颜色相同，则小明胜；如果转出的颜色可以配成紫色(一个转盘转出红色，另一个转盘转出蓝色)，则小亮胜，这个游戏对两人公平吗？请说明理由。

查看试题解析
20. 制造一种产品，原来每件成本价500元，销售价625元，经市场预测，两个月后销售价将下降15.2%，为保证利润不变，必须降低成本，问平均每个月下降成本的百分比是多少？

查看试题解析
21. 某商店购进一批单价为20元的日用商品，如果以单价30元销售，那么半月内可售出400件，根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件，如果提高售价，请问将售价定每件为多少元时，才能在半月内获得最大利润？并求出最大利润.

查看试题解析
22. 如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D，过点D作EF⊥AC，垂足为E，且交AB的延长线于点F.

(1)、求证：EF是⊙O的切线；

(2)、若AB＝10，∠A＝60°，求CD的长.

查看试题解析
23. 如图，点M， $N$ 分别在正方形 $A B C D$ 的边 $B C$ ， $C D$ 上，且 $∠ M A N = 45 °$ ，把 $△ A D N$ 绕点A顺时针旋转 $90 °$ 得到 $△ A B E$ .

(1)、求证： $△ A E M$ ≌ $△ A N M$ .

(2)、若 $B M = 3$ ， $D N = 2$ ，求正方形 $A B C D$ 的边长.

查看试题解析
24. 如图，已知抛物线y＝﹣x²+bx+c经过A（﹣1，0），B（3，0）两点.

(1)、求抛物线的解析式和顶点坐标；

(2)、当0＜x＜3时，直接写出y的取值范围；

(3)、点P为抛物线上一点，若S_△PAB＝10，求出此时点P的坐标.

查看试题解析