河南省信阳市息县2021-2022学年九年级上学期适应性测试数学试卷（二）

试卷更新日期：2022-01-19 类型：月考试卷

进入出卷网下载

一、单选题

1. 2021年3月20日三星堆遗址的最新考古发现又一次让世界为之瞩目，下列三星堆文物图案中，既是中心对称图形也是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系xOy中，点P（2x－1，x＋3）关于原点成中心对称的点的坐标在第四象限内，则x的取值范围是（）

A、 $x < \frac{1}{2}$ B、 $- 3 < x < \frac{1}{2}$ C、 $x > \frac{1}{2}$ D、x＞－3

查看试题解析
3. 如图，AB是⊙O的直径，C ， D为⊙O上的点， $\overset{⌢}{A D} = \overset{⌢}{C D}$ ，如果∠CAB＝40°，那么∠CAD的度数为（）

A、25° B、50° C、40° D、80°

查看试题解析
4. 扬帆中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为 $x m$ ，则可列方程为（）

A、 $(30 - x) (20 - x) = \frac{3}{4} \times 20 \times 30$ B、 $(30 - 2 x) (20 - x) = \frac{1}{4} \times 20 \times 30$ C、 $30 x + 2 \times 20 x = \frac{1}{4} \times 20 \times 30$ D、 $(30 - 2 x) (20 - x) = \frac{3}{4} \times 20 \times 30$

查看试题解析
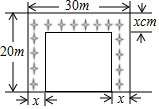5. 已知点A（－1，y₁），B（2，y₂），C（－3，y₃）在抛物线y＝－x²＋2x＋c上，则下列结论正确的是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
6. 如图，在 ⊙O中， $\overset{⌢}{A C} = \overset{⌢}{B C}$ ， D、E分别是半径OA，OB的中点，连接OC，AC，BC，CD，CE，则下列结论不一定成立的是（）

A、AC＝BC B、CD＝CE C、∠ACD＝∠BCE D、CD⊥OA

查看试题解析
7. 定义运算：a※b＝a²－2ab＋1，例如：4※2＝4²－2×4×2＋1＝1，则方程x※2＝－4的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定

查看试题解析
8. 将抛物线y＝x²－2x－1向右平移1个单位长，再向上平移3个单位长，平移后的解析式为y＝x²＋bx＋c，则b、c 的值分别为（）

A、b＝－2，c＝2 B、b＝－4，c＝－4 C、b＝－4，c＝5 D、b＝0，c＝2

查看试题解析
9. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α(0°＜α＜90°).若∠1＝112°，则∠α的大小是（）

A、68° B、20° C、28° D、22°

查看试题解析
10. 如图，抛物线y＝ax²+bx+c与x轴相交于A.B两点，点A在点B左侧，顶点在折线M﹣P﹣N上移动，它们的坐标分别为M（﹣1，4）.P（3，4）.N（3，1）.若在抛物线移动过程中，点A横坐标的最小值为﹣3.则a﹣b+c的最小值是（）

A、﹣15 B、﹣12 C、﹣4 D、﹣2

查看试题解析

二、填空题

11. 写出一个一元二次方程，使方程其中一个根为0.

查看试题解析
12. 如图，△ODC是由△OAB绕点O顺时针旋转40°后得到的图形，若点D恰好落在AB上，且∠AOC=105°，则∠C=°.

查看试题解析
13. 若二次函数y＝2（x+1）²+3的图象上有三个不同的点A（x₁ ， 4）、B（x₁+x₂ ， n）、C（x₂ ， 4），则n的值为.

查看试题解析
14. 如图，矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于 $O$ ，以 $B$ 为圆心、 $B C$ 长为半径画弧，交 $A B$ 于点 $F$ ，若点 $O$ 恰好在圆弧上，且 $A B = 6 \sqrt{3}$ ，则阴影部分的面积为.

查看试题解析
15. 如图，长方形ABCD中AB＝2，BC＝4，正方形AEFG的边长为1．正方形AEFG绕点A旋转的过程中，线段CF的长的最小值为．

查看试题解析

三、解答题

16. 解下列方程：

(1)、x²－4x＝1

(2)、x（x＋1）＝2＋2x

查看试题解析
17. 如图，△ABC三个顶点的坐标分别为A（－1，1），B（－2，4），C（－4，3）.

(1)、请画出△ABC绕原点顺时针旋转 $90 °$ 后得到的△A'B'C'；

(2)、点C'的坐标是；

(3)、在（1）的条件下，点A经过的路径的长度为（结果保留π）.

查看试题解析
18. 已知关于 $x$ 的一元二次方程：x²－mx＋m－2＝0

(1)、证明：无论m为何值，原方程有两个不相等的实数根；

(2)、若方程的一个根为2，求m的值及方程的另一根.

查看试题解析
19. 有一条长 $40 m$ 的篱笆如何围成一个面积为 $75 m^{2}$ 的矩形场地？能围成一个面积为 $101 m^{2}$ 的矩形场地吗？如能，说明围法；如不能，说明理由.

查看试题解析
20. 某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元．经市场调查，每天的销售量y(千克)与每千克售价x(元)满足一次函数关系，部分数据如下表：

售价x/(元/千克)

50

60

70

销售量y/千克

100

80

60

(1)、求y与x之间的函数表达式；

(2)、设商品每天的总利润为W(元)，求W与x之间的函数表达式(利润＝收入－成本)；

(3)、试说明(2)中总利润W随售价x的变化而变化的情况，并指出售价为多少时获得最大利润，最大利润是多少？

查看试题解析
21. 已知 $△ A B C$ 内接于 $⊙ O ， A B = A C ， ∠ B A C = 42 °$ ，点D是 $⊙ O$ 上一点.

(1)、如图①，若 $B D$ 为 $⊙ O$ 的直径，连接 $C D$ ，求 $∠ D B C$ 和 $∠ A C D$ 的大小；

(2)、如图②，若 $C D$ // $B A$ ，连接 $A D$ ，过点D作 $⊙ O$ 的切线，与 $O C$ 的延长线交于点E，求 $∠ E$ 的大小.

查看试题解析
22. 如图，已知二次函数y＝﹣x²+bx+c的图象经过点A（3，1），点B（0，4）.

(1)、求该二次函数的表达式及顶点坐标；

(2)、点C（m，n）在该二次函数图象上.
①当m＝﹣1时，求n的值；
②当m≤x≤3时，n最大值为5，最小值为1，请根据图象直接写出m的取值范围.

查看试题解析
23. 如图①，正方形ADEF中，∠DAF＝90°，点B、C分别在边AD、AF上，且AB＝AC，

(1)、FC和BD的关系是：；

(2)、如图②，当△ABC绕点A逆时针旋转α（0°＜α＜180°）时，那么（1）中结论还成立吗？若成立，请证明；若不成立，请说明理由；

(3)、如图③△ABC绕点A逆时针旋转45°时，延长DB交CF于点H；当AB＝2，AD＝ $\sqrt{3}$ ＋ $\sqrt{2}$ 时，请直接写出线段FH的长.

查看试题解析

售价x/(元/千克)	50	60	70
销售量y/千克	100	80	60