河南省信阳市罗山县2021-2022学年九年级上学期第三次月考数学试卷
试卷更新日期:2022-01-19 类型:月考试卷
一、单选题
-
1. “致中和,天地位焉,万物育焉.”对称美是我同古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊绝了千年的时光.在下列标识或简图中为既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线 的顶点坐标是( )A、(3, -5) B、(-3, 5) C、(3, 5) D、(-3, -5)3. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠14. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、5. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①、②、③、④的某个位置,使它与原来7个小正方形组成的图形是中心对称图形.这个位置是( )
2. 抛物线 的顶点坐标是( )A、(3, -5) B、(-3, 5) C、(3, 5) D、(-3, -5)3. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠14. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、5. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①、②、③、④的某个位置,使它与原来7个小正方形组成的图形是中心对称图形.这个位置是( )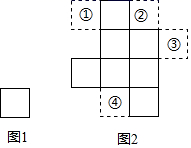 A、① B、② C、③ D、④6. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A、① B、② C、③ D、④6. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( ) A、 B、1 C、 D、7. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、8. 二次函数(a,b,c为常数,且)中的x与y的部分对应值如表.下列结论:①;②当时,y的值随x值的增大而减小③3是方程的一个根;④当时,.其中正确的个数为( )
A、 B、1 C、 D、7. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、8. 二次函数(a,b,c为常数,且)中的x与y的部分对应值如表.下列结论:①;②当时,y的值随x值的增大而减小③3是方程的一个根;④当时,.其中正确的个数为( )x
…
-1
0
1
3
…
y
…
-1
3
5
3
…
A、1个 B、2个 C、3个 D、4个9. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , ,将 绕点O逆时针旋转 ,点B的对应点B的坐标是( )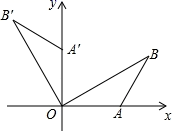 A、 B、 C、 D、10. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
A、 B、 C、 D、10. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 已知点 , 关于原点对称,则 .12. 疫情防控期间,各学校严格落实测体温进校园的防控要求,某学校开设了 , , 三个测温通道.某天早晨,小明和小红两位同学随机通过测温通道进入校园,则小明和小红从同一通道进入校园的概率为 .13.
如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= .
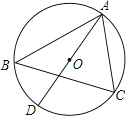 14. 将二次函数的图象沿x轴向右平移2个单位长度,得到的函数解析式是.15. 如图,是等腰直角三角形, , , 把绕点A按顺时针方向旋转后得到 , 则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是.
14. 将二次函数的图象沿x轴向右平移2个单位长度,得到的函数解析式是.15. 如图,是等腰直角三角形, , , 把绕点A按顺时针方向旋转后得到 , 则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是.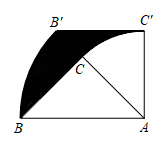
三、解答题
-
16. 阅读下列“问题”与“提示”后,将解方程的过程补充完整,求出x的值.
解方程:
提示:可以用“换元法”解方程.
解;设 , 则有.
原方程可化为:
续解:
17. 从2021年起,江苏省高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.(1)、若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是;(2)、若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.18. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点、、均在格点上. (1)、将向下平移5个单位得到 , 并写出点的坐标;(2)、画出绕点逆时针旋转90°后得到的 , 并写出点的坐标;(3)、在(2)的条件下,求在旋转过程中扫过的面积(结果保留).19. 如图,AB是半圆O的直径,AC是半圆内一条弦,点D是弧AC的中点,DB交AC于点G.过点A作半圆的切线与BD的延长线交于点M,连接AD,点E是AB上的一动点,DE与AC相交于点F.
(1)、将向下平移5个单位得到 , 并写出点的坐标;(2)、画出绕点逆时针旋转90°后得到的 , 并写出点的坐标;(3)、在(2)的条件下,求在旋转过程中扫过的面积(结果保留).19. 如图,AB是半圆O的直径,AC是半圆内一条弦,点D是弧AC的中点,DB交AC于点G.过点A作半圆的切线与BD的延长线交于点M,连接AD,点E是AB上的一动点,DE与AC相交于点F.
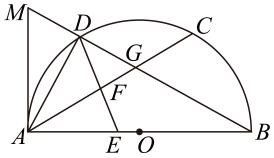 (1)、求证:;(2)、填空:①当时,;
(1)、求证:;(2)、填空:①当时,;②若的度数为 , 当时,四边形DEBC是菱形.
20. 已知关于x的一元二次方程 。(1)、求证:方程有两个不相等的实数根;(2)、若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。21. 某商店销售甲、乙两种商品,现有如下信息:信息1:甲、乙两种商品的进货单价之和是3元;
信息2:按商品的进货单价购买甲商品3件和乙商品2件,共付了7元
请结合以上信息,解答下列问题:
(1)、求甲、乙两种商品的进货单价:(2)、已知甲、乙两种商品的零售单价分別为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商品决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价进货单价)22. 已知抛物线(a,b,c是常数,)的自变量x与函数值y的部分对应值如下表:x
…
-2
-1
0
1
2
…
y
…
m
0
-3
n
-3
…
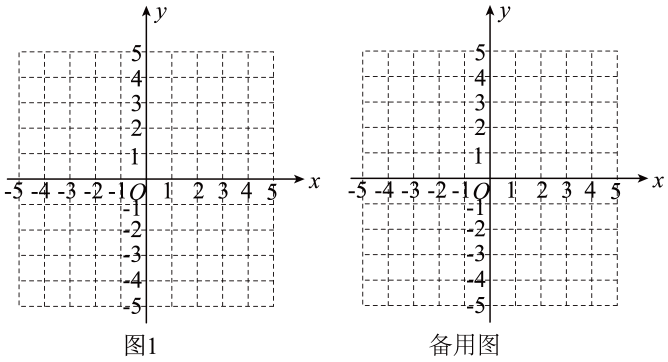 (1)、根据以上信息,可知抛物线开口向 , 对称轴为;(2)、求抛物线的表达式及m,n的值;(3)、请在图1中画出所求的抛物线,设点P为抛物线上的动点,OP的中点为 , 描出5个相应的点 , 再把相应的点用平滑的曲线连接起来,猜想该曲线是哪种曲线?(4)、设直线与抛物线及(3)中的点所在曲线都有两个交点,交点从左到右依次为 , , , , 请根据图象直接写出线段的值为.23. 小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,与恰好为对顶角, , 连接 , , 点F是线段上一点.
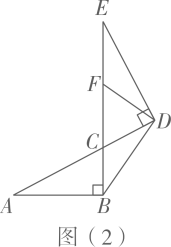
(1)、根据以上信息,可知抛物线开口向 , 对称轴为;(2)、求抛物线的表达式及m,n的值;(3)、请在图1中画出所求的抛物线,设点P为抛物线上的动点,OP的中点为 , 描出5个相应的点 , 再把相应的点用平滑的曲线连接起来,猜想该曲线是哪种曲线?(4)、设直线与抛物线及(3)中的点所在曲线都有两个交点,交点从左到右依次为 , , , , 请根据图象直接写出线段的值为.23. 小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,与恰好为对顶角, , 连接 , , 点F是线段上一点.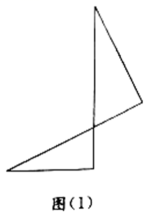
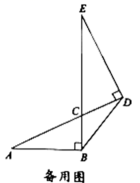 (1)、探究发现:
(1)、探究发现:
当点F为线段的中点时,连接 , 如图(2),小明经过探究,得到结论:.你认为此结论是否成立?.(填“是”或“否”)(2)、拓展延伸:
将(1)中的条件与结论互换,即:若 , 则点F为线段的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.(3)、问题解决:
若 , 求的长.