2022年苏科版初中数学《中考一轮复习》专题五 图形的变换 5.3 图形的平移和旋转
试卷更新日期:2022-01-18 类型:一轮复习
一、单选题
-
1. 如图所示,将△ABC绕点A逆时针旋转至△ADE,则旋转角为( ).
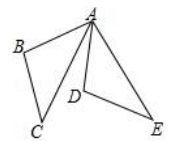 A、∠BAD B、∠BAC C、∠BAE D、∠CAD2. 如图,将△ABC绕点A逆时针旋转120°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( )
A、∠BAD B、∠BAC C、∠BAE D、∠CAD2. 如图,将△ABC绕点A逆时针旋转120°,得到△ADE.若点D在线段BC的延长线上,则 的大小为( ) A、30° B、40° C、50° D、60°3. 如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是5,则图中阴影部分的面积为( )
A、30° B、40° C、50° D、60°3. 如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是5,则图中阴影部分的面积为( ) A、25 B、50 C、35 D、704. 如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,那么∠AOB'的度数是( )
A、25 B、50 C、35 D、704. 如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,那么∠AOB'的度数是( )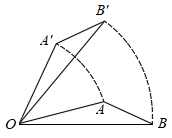 A、15° B、30° C、45° D、60°5. 如图,将ABC绕点A按逆时针方向旋转得到 . 使点恰好落在BC边上,∠BAC=120°,= , 则∠C的度数为( )
A、15° B、30° C、45° D、60°5. 如图,将ABC绕点A按逆时针方向旋转得到 . 使点恰好落在BC边上,∠BAC=120°,= , 则∠C的度数为( ) A、18° B、20° C、24° D、28°6. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , , 将绕点O逆时针旋转 , 点B的对应点的坐标是( )
A、18° B、20° C、24° D、28°6. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上, , , 将绕点O逆时针旋转 , 点B的对应点的坐标是( )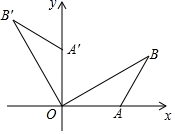 A、 B、 C、 D、7. 如图,已知二次函数 向右平移2个单位得到抛物线 的图象,则阴影部分的面积为( )
A、 B、 C、 D、7. 如图,已知二次函数 向右平移2个单位得到抛物线 的图象,则阴影部分的面积为( ) A、3 B、4 C、5 D、68. 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点P在△ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP = 6,则PC的最小值是( )
A、3 B、4 C、5 D、68. 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点P在△ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP = 6,则PC的最小值是( )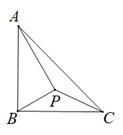 A、 B、 C、 D、9. 如图,在平面直角坐标系中,Q是直线y=﹣ x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点 ,连接 ,则 的最小值为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,Q是直线y=﹣ x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点 ,连接 ,则 的最小值为( ) A、 B、 C、 D、10. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )
A、 B、 C、 D、10. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )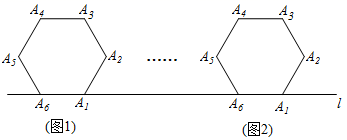 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,将 沿 方向平移至 处.若 ,则 = .
 12. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=10.如果将△ABC绕点C按逆时针旋转到△A′B′C的位置,并且点B恰好落在边A′B′上,则BB′的长为 .
12. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=10.如果将△ABC绕点C按逆时针旋转到△A′B′C的位置,并且点B恰好落在边A′B′上,则BB′的长为 .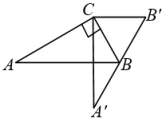 13. 如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得C′C∥AB , 则∠BAB′等于 .
13. 如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得C′C∥AB , 则∠BAB′等于 . 14. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .
14. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .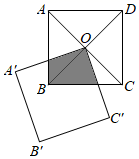 15. 在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,则图中阴影部分的面积是 .
15. 在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,则图中阴影部分的面积是 .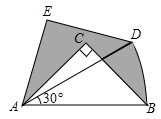 16. 在如图所示的正方形网格中, 绕某点旋转一定的角度,得到 ,则旋转中心可能是A,B,C,D中的点 .
16. 在如图所示的正方形网格中, 绕某点旋转一定的角度,得到 ,则旋转中心可能是A,B,C,D中的点 .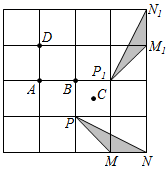 17. 如图,在 中, , ,点D为 内一点, , ,连接AD,将 绕点C按逆时针方向旋转,使CA与CB重合,点D的对应点为点E,连接DE,DE交BC于点F,则BF的长为cm.
17. 如图,在 中, , ,点D为 内一点, , ,连接AD,将 绕点C按逆时针方向旋转,使CA与CB重合,点D的对应点为点E,连接DE,DE交BC于点F,则BF的长为cm. 18. 如图,将矩形OABC置于平面直角坐标系xOy中, , .抛物线y=﹣x2+bx+c经过点B,C,顶点为D.将矩形OABC绕原点顺时针旋转一个角度θ(0°<θ<360°),得到矩形OA'B'C',记A'C'的中点E,连结DE,线段DE的长度最大值为 .
18. 如图,将矩形OABC置于平面直角坐标系xOy中, , .抛物线y=﹣x2+bx+c经过点B,C,顶点为D.将矩形OABC绕原点顺时针旋转一个角度θ(0°<θ<360°),得到矩形OA'B'C',记A'C'的中点E,连结DE,线段DE的长度最大值为 .
三、综合题
-
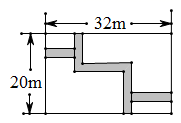
19. 如图所示,某住宅小区内有一块长的长 ,宽 方形形,想在长方形地块内修筑同样宽的两条“之”字路,余下的部分做绿化,道路的宽为 米,求绿化的面积.
 20. 如图将 绕点A逆时针旋转得到 ,点C和点E是对应点,若 , ,求BD的长.
20. 如图将 绕点A逆时针旋转得到 ,点C和点E是对应点,若 , ,求BD的长. 21. 如图,点O是等边三角形ABC内部一点,且满足∠BOC=150°,将△BOC绕点C按顺时针旋转至△ADC的位置,连接OD,OA.
21. 如图,点O是等边三角形ABC内部一点,且满足∠BOC=150°,将△BOC绕点C按顺时针旋转至△ADC的位置,连接OD,OA. (1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.22. 如图1所示,在 中, , ,P是BC边上一点(不与B、C点重合),将线段AP绕点A逆时针旋转 得到扇形PAQ.
(1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.22. 如图1所示,在 中, , ,P是BC边上一点(不与B、C点重合),将线段AP绕点A逆时针旋转 得到扇形PAQ. (1)、求证:(2)、当BC与扇形PAQ相切时,求BQ的长;(3)、如图2,若 ,求阴影部分的图形的周长.(结果不求近似值)23. 如图1,在 ABC中,CA=CB,∠ACB=90°,D是 ABC内部一点,∠ADC=135°,将线段CD绕点C逆时针旋转90°,得到线段CE,连接DE.
(1)、求证:(2)、当BC与扇形PAQ相切时,求BQ的长;(3)、如图2,若 ,求阴影部分的图形的周长.(结果不求近似值)23. 如图1,在 ABC中,CA=CB,∠ACB=90°,D是 ABC内部一点,∠ADC=135°,将线段CD绕点C逆时针旋转90°,得到线段CE,连接DE. (1)、求∠CDE的度数,并说明A、D、E三点是否共线;(2)、在(1)的条件下,连接BE,如图2,过点C作CM⊥DE于点M,请判断线段AE,CM和BE之间的数量关系,并说明理由.24. 有公共顶点A的△ABD , △ACE都是的等边三角形.
(1)、求∠CDE的度数,并说明A、D、E三点是否共线;(2)、在(1)的条件下,连接BE,如图2,过点C作CM⊥DE于点M,请判断线段AE,CM和BE之间的数量关系,并说明理由.24. 有公共顶点A的△ABD , △ACE都是的等边三角形.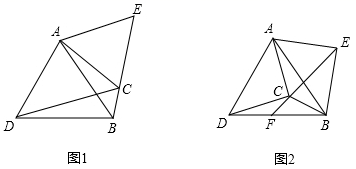 (1)、如图1,将△ACE绕顶点A旋转,当E , C , B共线时,求∠BCD的度数;(2)、如图2,将△ACE绕顶点A旋转,当∠ACD=90°时,延长EC角BD于F ,
(1)、如图1,将△ACE绕顶点A旋转,当E , C , B共线时,求∠BCD的度数;(2)、如图2,将△ACE绕顶点A旋转,当∠ACD=90°时,延长EC角BD于F ,①求证:∠DCF=∠BEF;
②写出线段BF与DF的数量关系,并说明理由.
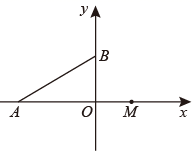
25. 如图,在平面直角坐标系中,已知点A(a,0) , .(Ⅰ)如图,若 ,已知点 .

①连接AC , 当 轴时,求m的值:
②若 的面积是8,求m的值:
(Ⅱ)如图,若 ,射线BA以每秒9°的速度绕点B顺时针方向旋转至射线BA1 , 点M为x轴正半轴上一点,射线MO以每秒6°的速度绕点M逆时针方向旋转到MO1 , 设运动时间为t秒 ,求t为多少秒时,直线 ?
 26. 如图,将两个等腰直角三角形纸片 和 放置在平面直角坐标系中,点 ,点 ,点 ,点 ,点 .
26. 如图,将两个等腰直角三角形纸片 和 放置在平面直角坐标系中,点 ,点 ,点 ,点 ,点 .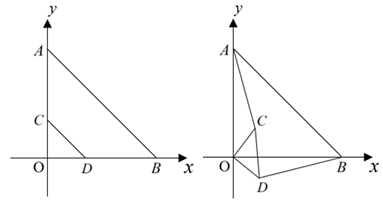 (1)、求证: ;(2)、如图,现将 绕点O顺时针方向旋转,旋转角为 ,连接 , ,这一过程中 和 是否仍然保持相等?说明理由;当旋转角 的度数为时, 所在直线能够垂直平分 ;(3)、在(2)的情况下,将旋转角 的范围扩大为 ,那么在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.(直接写出结果即可).27. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
(1)、求证: ;(2)、如图,现将 绕点O顺时针方向旋转,旋转角为 ,连接 , ,这一过程中 和 是否仍然保持相等?说明理由;当旋转角 的度数为时, 所在直线能够垂直平分 ;(3)、在(2)的情况下,将旋转角 的范围扩大为 ,那么在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.(直接写出结果即可).27. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .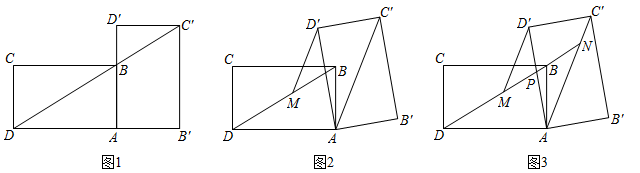
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
28. 如图 ,已知点G在正方形ABCD的对角线AC上, ,垂足为点E, ,垂足为点F.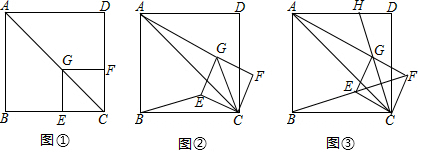 (1)、发现问题:在图 中, 的值为.(2)、探究问题:将正方形CEGF绕点C顺时针方向旋转 角 ,如图 所示,探究线段AG与BE之间的数量关系,并证明你的结论.(3)、解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图 所示,延长CG交AD于点H;若 , ,直接写出BC的长度.
(1)、发现问题:在图 中, 的值为.(2)、探究问题:将正方形CEGF绕点C顺时针方向旋转 角 ,如图 所示,探究线段AG与BE之间的数量关系,并证明你的结论.(3)、解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图 所示,延长CG交AD于点H;若 , ,直接写出BC的长度.