2022年苏科版初中数学《中考一轮复习》专题五 图形的变换 5.2 图形的对称
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 下列产品logo图片中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 如图，在△ABC中，AB＝8cm，BC＝6cm，AC＝5cm.沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED 的周长是（ ）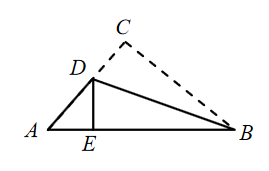
A、5cm B、6cm C、7cm D、8cm3. 如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在点D处，已知 ，则点D的坐标为（ ）
A、 B、 C、 D、4. 如图， 内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点.若GH的长为15cm，则 的周长为（ ）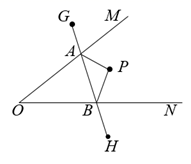
A、5cm B、10cm C、20cm D、15cm5. 如图，有一张四边形纸片ABCD，AD∥BC，将它沿GH折叠，使点D落在AB边上的点E处，点C落在点Q处，若∠GHB＝80°，则∠AGE的度数为（ ）
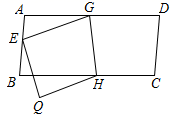A、20° B、30° C、35° D、40°6. 把一张对边互相平行的纸条按如图所示折叠，EF是折痕，若∠EFB＝34°，则下列结论不正确的是（ ）
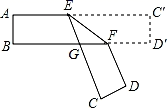A、 B、∠AEC＝146° C、∠BGE＝68° D、∠BFD＝112°7. 如图，将矩形纸条ABCD折叠，折痕为EF，折叠后点C，D分别落在点C′，D′处，D′E与BF交于点G.已知∠BGD′＝30°，则∠α的度数是（ ）
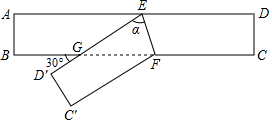A、30° B、45° C、74° D、75°8. 如图，在矩形纸片ABCD中，点E、F分别在矩形的边AB、AD上，将矩形纸片沿CE、CF折叠，点B落在H处，点D落在G处，点C、H、G恰好在同一直线上，若AB＝6，AD＝4，BE＝2，则DF的长是（ ）
A、2 B、 C、 D、39. 如图，在△ABC中，AB＝AC，∠BAC＝46°，∠BAC的平分线与AB的垂直平分线OD交于点O，点E在BC上，点F在AC上，连接EF.将∠C沿EF折叠，点C与点O恰好重合时，则∠OEC的度数（ ）
A、90° B、92° C、95° D、98°10. 如图，将三角形纸片ABC沿DE折叠，使B与C重合，CD ， AE相交于F ， 已知BD＝4AD ， 设△ABC的面积为S ， △CEF的面积为S1 ， △ADF的面积为S2 ， 则 的值为（ ）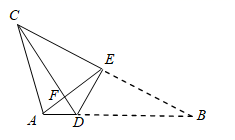
A、 B、 C、 D、二、填空题
-
11. 如图所示，将矩形ABCD沿AE折叠，若 ， 则等于.
12. 如图，△ABC中，∠A=60°将△ABC沿DE翻折后，点A落在BC边上的点A′处．如果∠A′DB=50°，那么∠A′ED的度数为 ．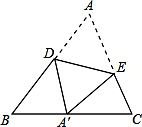
13. 动手操作：在长方形纸片ABCD中，AB＝6，AD＝10．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ ， 当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为 ．
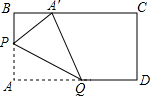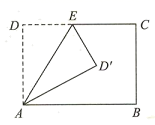
14. 在如图所示的正方形网格中， 绕某点旋转一定的角度，得到 ，则旋转中心可能是A，B，C，D中的点 ．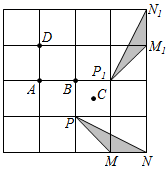
15. 如图，在矩形ABCD中， ，点E ， F分别在BC ， CD上，将 沿AE折叠，使点B落在AC上的点 处，又将 沿EF折叠，使点C落在直线 与AD的交点 处， ．
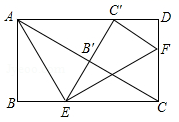16. 如图坐标系中，O（0，0），A（3，3 ），B（6，0），将△OAB沿直线CD折叠，使点A恰好落在线段OB上的点E处，若OE＝ ，则AC：AD的值是.
17. 如图， 是 的直径， ，点 在 上， ， 是 的中点， 是直径 上的一动点，若 ，则 周长的最小值为.
18. 如图，四边形ABCD为矩形，AB＝ ，AD＝ ，点P为边AB上一点．以DP为折痕将△DAP翻折，点A的对应点为点A'．连结AA'，AA' 交PD于点M ， 点Q为线段BC上一点，连结AQ ， MQ ， 则AQ＋MQ的最小值是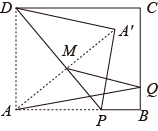
三、综合题
-
19. 如图，已知四边形 ，
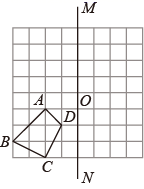(1)、画出四边形 向上平移5格后的四边形 ；(2)、画出四边形 关于点O成中心对称的四边形 ：(3)、画出四边形 关于直线 成轴对称的四边形 ；(4)、四边形 与四边形 是否对称？若对称，在图中画出对称轴或对称中心.20. 如图，在长方形ABCD中，DC=9，在DC上找一点E，沿直线AE把△AED折叠，使D点恰好落在BC上，设这一点为F，若OABF的面积是54，求DE的长．
21. 如图所示，长方形ABCD中，AB=6cm，BC=8cm，将长方形对折，使B点与D点重合，它的折痕为EF，求图中CE的长．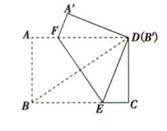
22. 如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长.
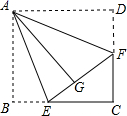23. 如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处.求∠1+∠2的度数.
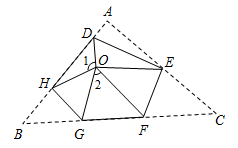24. 如图，将 ABC分别沿AB ， AC翻折得到 ABD和 AEC ， 线段BD与AE交于点F ， 连接BE ．
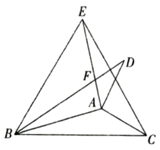(1)、若∠ABC=20°，∠ACB=30°，求∠DAE及∠BFE的度数．(2)、若BD所在的直线与CE所在的直线互相垂直，求∠CAB的度数．25. 已知点P在∠MON内．
(1)、如图1，点P关于射线OM的对称点是G，点P关于射线ON的对称点是H，连接OG、OH、OP．①若∠MON=50°，则∠GOH= ▲ ；
②若PO=5，连接GH，请说明当∠MON为多少度时，GH=10；
(2)、如图2，若∠MON=60°，A、B分别是射线OM、ON上的任意一点，当 PAB的周长最小时，求∠APB的度数．26. 在四边形ABCD中，∠A＝∠B＝∠C＝∠D＝90°，AB＝CD＝10，BC＝AD＝8.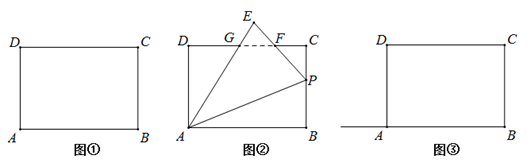
(1)、P为BC上一点，将△ABP沿直线AP翻折至△AEP的位置（点B落在点E处）.①如图①，当点E落在边CD上时，利用尺规作图，在图①中作出满足条件的图形（即△AEP的位置，不写作法，保留作图痕迹），并直接写出此时DE＝ .
②如图②，PE与CD相交于点F，AE与CD相交于点G，且FC＝FE，求BP的长.
(2)、如图③，已知点Q为射线BA上的一个动点，将△BCQ沿CQ翻折，点B恰好落在直线DQ上的点B’处，求BQ的长.27. 实践与探究(1)、操作一：如图①，已知正方形纸片ABCD，将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，则 度.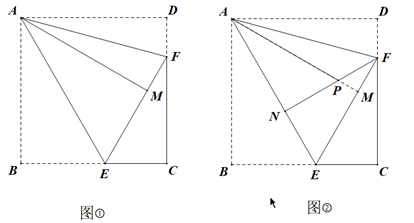
操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N.我们发现，当点E的位置不同时，点N的位置也不同.当点E在BC边的某一位置时，点N恰好落在折痕AE上，则 度.
(2)、在图②中，运用以上操作所得结论，解答下列问题：设AM与NF的交点为点P.求证 ：.
(3)、若 ，则线段AP的长为.28. 已知正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC于点M、N，AH⊥MN于点H.
(1)、如图①，当BM＝DN时，请你通过证明△ADN≌△ABM，得到AH与AB的数量关系，这个数量关系是；(2)、如图②，当BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？说明理由；(3)、如图③，已知△AMN中，∠MAN＝45°，AH⊥MN于点H，且MH＝3，NH＝7，求AH的长.