2022年苏科版初中数学《中考一轮复习》专题五 图形的变换 5.1 图形的展开与折叠
试卷更新日期:2022-01-18 类型:一轮复习
一、单选题
-
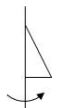
1. 在图形的旋转中,下列说法错误的是( )A、旋转前和旋转后的图形全等 B、图形上的每一个点到旋转中心的距离都相等 C、对应点与旋转中心所连线段的夹角等于旋转角 D、图形上可能存在不动的点2. 如下图,将三角形绕轴旋转一周,所得的立体图形从正面观察得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各图中,可以是一个正方体的平面展开图的是( )A、
3. 下列各图中,可以是一个正方体的平面展开图的是( )A、 B、
B、 C、
C、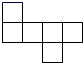 D、
D、 4. 如图是一个正方体的表面展开图,则原正方体标有数字“ ”所在面的对面标有的数字是( )
4. 如图是一个正方体的表面展开图,则原正方体标有数字“ ”所在面的对面标有的数字是( )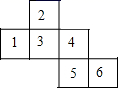 A、2 B、4 C、5 D、65. 如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A、2 B、4 C、5 D、65. 如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( ) A、正方体、圆柱、三棱锥 B、正方体、三棱锥、圆柱 C、正方体、圆柱、三棱柱 D、三棱锥、圆锥、正方体6. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )
A、正方体、圆柱、三棱锥 B、正方体、三棱锥、圆柱 C、正方体、圆柱、三棱柱 D、三棱锥、圆锥、正方体6. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )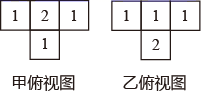 A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同7. 某三棱锥的三视图如图所示,该三棱锥的体积是( )
A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同7. 某三棱锥的三视图如图所示,该三棱锥的体积是( )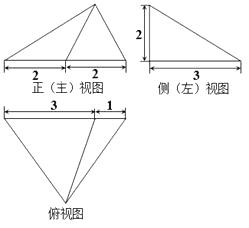 A、 B、4 C、2 D、8. 小欣同学用纸(如图)折成了个正方体的盒子,里面放了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中( )
A、 B、4 C、2 D、8. 小欣同学用纸(如图)折成了个正方体的盒子,里面放了一瓶墨水,混放在下面的盒子里,只凭观察,选出墨水在哪个盒子中( ) A、
A、 B、
B、 C、
C、 D、
D、 9.
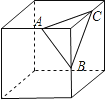
9.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
 A、
A、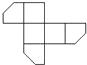
B、
B、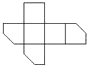
C、
C、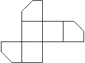
D、
D、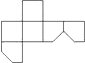
10. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
10. 如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )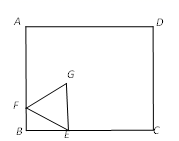 A、3 B、2.5 C、4 D、2
A、3 B、2.5 C、4 D、2二、填空题
-
11. 如图,是小明同学在数学实践课上,所设计的正方体盒子的平面展开图,每个面上都有一个汉字,请你判断,正方体盒子上与“答”字相对的面上的字是.
 12. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面 , 如果正方体的左面与右面所标注式子的值相等,则x的值为 .
12. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面 , 如果正方体的左面与右面所标注式子的值相等,则x的值为 . 13. 如图,一个正方块的六个面分别标有A,B,C,D,E,F,从三个不同方向看到的情况如图所示,则A的对面应该是.
13. 如图,一个正方块的六个面分别标有A,B,C,D,E,F,从三个不同方向看到的情况如图所示,则A的对面应该是.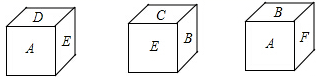 14. 如图是由一些相同的小正方体构成的立体,图形的三种视图构成这个立体图形的小正方体的个数是。
14. 如图是由一些相同的小正方体构成的立体,图形的三种视图构成这个立体图形的小正方体的个数是。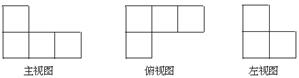 15. 用一些完全相同的正方体木块搭几何体,从其正面和上面看到的形状图如图所示,则搭成这个几何体所用正方体木块的个数最少为 .
15. 用一些完全相同的正方体木块搭几何体,从其正面和上面看到的形状图如图所示,则搭成这个几何体所用正方体木块的个数最少为 .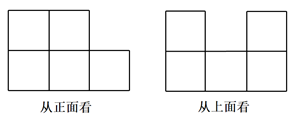 16. 如图,是一个多面体的表面展开图,每个面内都标注了字母,如果面A在多面体的底部,那么从上面看是面 . (填字母)
16. 如图,是一个多面体的表面展开图,每个面内都标注了字母,如果面A在多面体的底部,那么从上面看是面 . (填字母)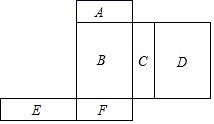 17. 如图是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为 .
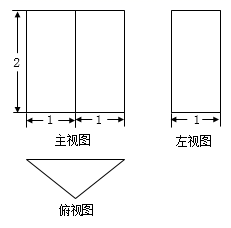
17. 如图是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为 .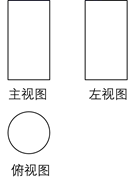 18. 从正面和左面看一个长方体得到的形状图如图所示(单位: ),则其从上面看到的形状图的面积为 .
18. 从正面和左面看一个长方体得到的形状图如图所示(单位: ),则其从上面看到的形状图的面积为 .
三、综合题
-
19. 如图是一个几何体的三视图,求该几何体的表面积.
 20. 长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
20. 长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少? 21. 如图
21. 如图 (1)、由大小相同的小立方块搭成的几何体如图,请在图中的方格中画出该几何体的俯视图和左视图.(2)、用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要个小立方块,最多要个小立方块.22. 用若干个大小相同的小立方块搭建一个几何体,从正面和上面观察这个几何体得到下面两幅形状图.
(1)、由大小相同的小立方块搭成的几何体如图,请在图中的方格中画出该几何体的俯视图和左视图.(2)、用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要个小立方块,最多要个小立方块.22. 用若干个大小相同的小立方块搭建一个几何体,从正面和上面观察这个几何体得到下面两幅形状图.

(从正面看) (从上面看)
(1)、请画出一种从左面看这个几何体得到的形状图;(2)、搭建这个几何体最少要用a=个小立方块,最多用b=个小立方块;(3)、在(2)的条件下,若有理数x,y满足 , ,且 ,求 的值.23. 用棱长都为5cm的小立方块搭成几何体,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.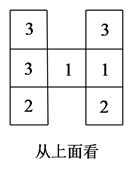 (1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;
(1)、请你分别画出从正面和从左面看到的这个几何体的形状图;(2)、若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)、①图中的几何体的表面积(包括与桌面接触的部分)为 ;②若新搭一个几何体,且满足如下三个条件:图中从上面看到的几何体的形状图不变,小立方块的总数不变,从上面看到的小正方形中的数字可以改变,则新搭几何体的表面积(包括与桌面接触的部分)最小值和最大值分别为 , .
24. 用棱长为 的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层, ,第 层( 为正整数)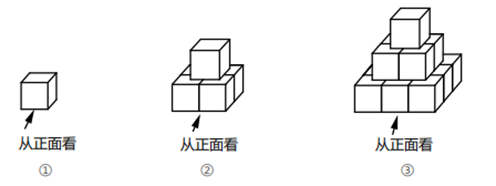 (1)、搭建第④个几何体的小立方体的个数为 .(2)、分别求出第②、③个几何体的所有露出部分(不含底面)的面积.(3)、为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?25. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)、搭建第④个几何体的小立方体的个数为 .(2)、分别求出第②、③个几何体的所有露出部分(不含底面)的面积.(3)、为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?25. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题: (1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.26. 在一次青少年模型大赛中,小高和小刘各制作了一个模型,小高制作的是棱长为acm的正方体模型,小刘制作的是棱长为acm的正方体右上角割去一个长为3cm,宽为2cm,高为1cm的长方体模型(如图2)
(1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.26. 在一次青少年模型大赛中,小高和小刘各制作了一个模型,小高制作的是棱长为acm的正方体模型,小刘制作的是棱长为acm的正方体右上角割去一个长为3cm,宽为2cm,高为1cm的长方体模型(如图2) (1)、用含a的代数式表示,小高制作的模型的各棱长度之和是;(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 ,求a的值;(3)、在(2)的条件下,
(1)、用含a的代数式表示,小高制作的模型的各棱长度之和是;(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 ,求a的值;(3)、在(2)的条件下,①图3是小刘制作的模型中正方体六个面的展开图,图中缺失的有一部分已经很用阴影表示,请你用阴影表示出其余缺失部分,并标出边的长度.
②如果把小刘的模型中正方体的六个面展开,则展开图的周长是 ▲ cm;请你在图方格中画出小刘的模型中正方体六个面的展开图周长最大时的图形.
