2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.11 正多边形与圆
试卷更新日期:2022-01-18 类型:一轮复习
一、单选题
-
1. 正十边形的每一个外角的度数都等于( )A、135° B、45° C、36° D、144°2. 下列命题正确的是( )A、正三角形的内切圆的半径与外接圆半径之比为2﹕1 B、正六边形的边长等于其外接圆的半径 C、圆的外切正多边形的边长等于其边心距的倍 D、各边相等的圆的外切四边形是正方形3. 如图,已知正五边形 内接于 ,连结 ,则 的度数是( )
 A、 B、 C、 D、4. 以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ).A、 B、 C、 D、5. 如图,要拧开一个边长为a=8mm的正六边形螺帽,扳手张开的开口b至少为( )
A、 B、 C、 D、4. 以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ).A、 B、 C、 D、5. 如图,要拧开一个边长为a=8mm的正六边形螺帽,扳手张开的开口b至少为( ) A、8 mm B、16mm C、8 mm D、4mm6. 一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,大正六边形在绕点O旋转过程中,下列说法正确的是( )
A、8 mm B、16mm C、8 mm D、4mm6. 一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,大正六边形在绕点O旋转过程中,下列说法正确的是( ) A、S变化,l不变 B、S不变,l变化 C、S变化,l变化 D、S与l均不变7. 如图,正方形ABCD和等边△AEF都内接于圆O,EF与BC,CD别相交于点G,H.若AE=6,则EG的长为( )
A、S变化,l不变 B、S不变,l变化 C、S变化,l变化 D、S与l均不变7. 如图,正方形ABCD和等边△AEF都内接于圆O,EF与BC,CD别相交于点G,H.若AE=6,则EG的长为( )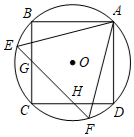 A、 B、3﹣ C、 D、2 ﹣38. 有一圆内接正八边形ABCDEFGH , 若△ADE的面积为10,则正八边形ABCDEFGH的面积为( )
A、 B、3﹣ C、 D、2 ﹣38. 有一圆内接正八边形ABCDEFGH , 若△ADE的面积为10,则正八边形ABCDEFGH的面积为( ) A、40 B、50 C、60 D、809.
A、40 B、50 C、60 D、809.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
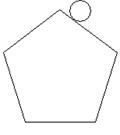 A、4 B、5 C、6 D、1010. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )
A、4 B、5 C、6 D、1010. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )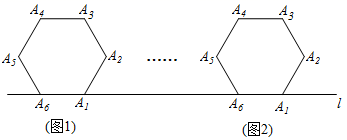 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知正多边形的一个内角为144°,则这个正多边形是正边形。12. 若正六边形的外接圆半径长为4,则它的边长等于 .13. 在正五边形的外接圆中,任一边所对的圆周角的度数为.14. 如图,⊙O的内接正六边形ABCDEF边长为 cm,则该正六边形的面积为cm2.
 15. 如图,正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上,正五边形在正六边形左侧,两个正多边形均在l的同侧,则 的大小是度.
15. 如图,正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上,正五边形在正六边形左侧,两个正多边形均在l的同侧,则 的大小是度.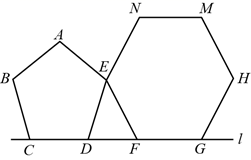 16. 如图,内接正八边形ABCDEFGH,若ΔADE的面积为10,则正八边形ABCDEFGH的面积为.
16. 如图,内接正八边形ABCDEFGH,若ΔADE的面积为10,则正八边形ABCDEFGH的面积为. 17. 如图, 与正六边形 的边 , 分别交于点 , ,点 为劣弧 的中点.若 ,则点 到 的距离是 .
17. 如图, 与正六边形 的边 , 分别交于点 , ,点 为劣弧 的中点.若 ,则点 到 的距离是 . 18. 如图,若干全等正五边形排成环状.图中所示的是前3个正五边形,要完成这一圆环还需 个正五边形.
18. 如图,若干全等正五边形排成环状.图中所示的是前3个正五边形,要完成这一圆环还需 个正五边形.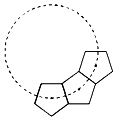
三、综合题
-
19. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
 20. 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
20. 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.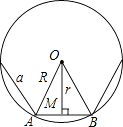 21. 如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
21. 如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.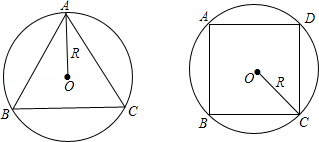 22. 已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形.
22. 已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形.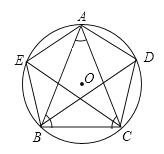 23. 中心为O的正六边形 的半径为 .点 同时分别从 两点出发,以 的速度沿 向终点 运动,连接 ,设运动时间为 .
23. 中心为O的正六边形 的半径为 .点 同时分别从 两点出发,以 的速度沿 向终点 运动,连接 ,设运动时间为 .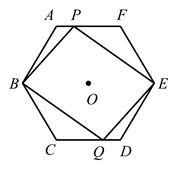 (1)、求证:四边形 为平行四边形;(2)、求矩形 的面积与正六边形 的面积之比.24. 如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.
(1)、求证:四边形 为平行四边形;(2)、求矩形 的面积与正六边形 的面积之比.24. 如图,正六边形ABCDEF中,点M在AB边上,∠FMH=120°,MH与六边形外角的平分线BQ交于点H.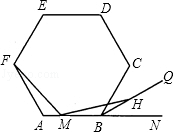 (1)、当点M不与点A、B重合时,求证:∠AFM=∠BMH.(2)、当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.25. 如图,正方形 内接于 , 为 上的一点,连接 , .
(1)、当点M不与点A、B重合时,求证:∠AFM=∠BMH.(2)、当点M在正六边形ABCDEF一边AB上运动(点M不与点B重合)时,猜想FM与MH的数量关系,并对猜想的结果加以证明.25. 如图,正方形 内接于 , 为 上的一点,连接 , . (1)、求 的度数;(2)、当点 为 的中点时, 是 的内接正 边形的一边,求 的值.26. 圆周率 的故事
(1)、求 的度数;(2)、当点 为 的中点时, 是 的内接正 边形的一边,求 的值.26. 圆周率 的故事我国古代数学家刘徽通过“割圆术”来估计圆周率 的值——“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,可以理解为当正多边形的边数越来越多时,该正多边形与它的外接圆越来越“接近”,这样就可以用正多边形的周长替代它的外接圆的周长,从而估算出圆周率 的值.
(1)、对于边长为a的正方形,其外接圆半径为 , 根据故事中的方法,用该正方形的周长4a替代它的外接圆周长,利用公式 ,可以估算 .(2)、类比(1),当正多边形为正六边形时,估计 的值.27. 如图(1),正五边形ABCDE与⊙O相切于点A,点C在⊙O上.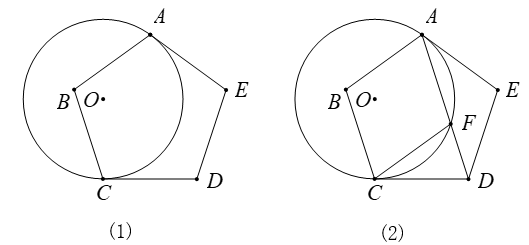 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为5,求劣弧AC的长度;(3)、如图(2),连接AD交⊙O于点F.求证:四边形ABCF是菱形.28. 某同学在学习了正多边形和圆之后,对正五边形的边及相关线段进行研究,发现多处出现者名的黄金分割比 .如图,圆内接正五边形 ,圆心为O, 与 交于点H, 、 与 分别交于点M、N.根据圆与正五边形的对称性,只对部分图形进行研究.(其它可同理得出)
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为5,求劣弧AC的长度;(3)、如图(2),连接AD交⊙O于点F.求证:四边形ABCF是菱形.28. 某同学在学习了正多边形和圆之后,对正五边形的边及相关线段进行研究,发现多处出现者名的黄金分割比 .如图,圆内接正五边形 ,圆心为O, 与 交于点H, 、 与 分别交于点M、N.根据圆与正五边形的对称性,只对部分图形进行研究.(其它可同理得出) (1)、求证: 是等腰三角形且底角等于36°,并直接说出 的形状;(2)、求证: ,且其比值 ;(3)、由对称性知 ,由(1)(2)可知 也是一个黄金分割数,据此求 的值.
(1)、求证: 是等腰三角形且底角等于36°,并直接说出 的形状;(2)、求证: ,且其比值 ;(3)、由对称性知 ,由(1)(2)可知 也是一个黄金分割数,据此求 的值.