2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.10 与圆有关的位置关系（2）
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 如图，AB和AC与圆O分别相切于点B和点C，点D是圆O上一点，若∠BAC＝74°，则∠BDC等于（ ）
A、46° B、53° C、74° D、106°2. 如图，AB是⊙O的切线，点B为切点，连接AO并延长交⊙O于点C，连接BC.若∠A＝26°，则∠C的度数为（ ）
A、26° B、32° C、52° D、64°3. 如图，AB为⊙O的切线，点A为切点，OB交⊙O于点C，点D在⊙O上，连接AD、CD、OA，若∠ADC=30°，则∠ABO的度数为（ ）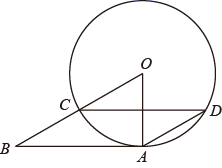
A、25° B、20° C、30° D、35°4. 如图，PA ， PB是⊙O的切线，AC是⊙O的直径，若∠BAC＝25°，则∠P的度数为( )
A、50° B、70° C、110° D、40°5. 如图，AB是⊙O的直径，点C在⊙O上，AE是⊙O的切线，A为切点，连接BC并延长交AE于点D.若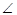
AOC=80°，则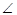ADB的度数为（ ）
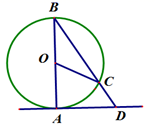A、40° B、50° C、60° D、20°6. 如图，在平面直角坐标系中，过边长为1的正方形格点A、B、C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（ ）
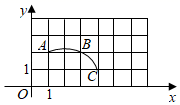A、点（5，0） B、点（2，3） C、点（6，1） D、点（1，3）7. 如图， 是 的直径，点C是 延长线上一点， 与 相切于点P，连接 ，若 ， ，则 的长是（ ）
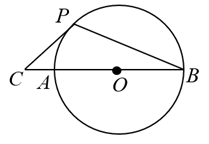A、 B、 C、 D、8. 如图， 为 的直径，直线 与 相切于点 ，点 为半圆弧 的中点，连接 交 于点 ，连接 ．若 ，则 的度数为（ ）
A、 B、 C、 D、9. 如图所示，在Rt 中， ， ， ，点 为 上的点， 的半径 ，点 是 边上的动点，过点 作⊙ 的一条切线 （点 为切点），则线段 的最小值为（ ）
A、
B、
C、
D、4
10. 如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（ ）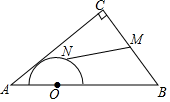
A、5 B、6 C、7 D、8二、填空题
-
11. 如图，PB与⊙O相切于点B，OP与⊙O相交于点A，若⊙O的半径为2，∠P＝30°，则OP的长为 ．
12. 如图所示，AB，AC与⊙O相切于点B，C，∠A=50°，点P是圆上异于B，C的一动点，则∠BPC的度数是 ．
13. 如图，等边三角形ABC的边长为4，E、F分别是边AB，BC上的动点，且AE＝BF，连接EF，以EF为直径作圆O.当圆O与AC边相切时，AE的长为.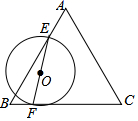
14. 如图，AB与⊙O相切于点B，连接AO并延长，交⊙O于点C，连接BC，若OA=2OC=2，则AB=.
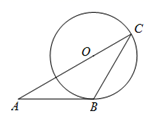15. 如图，直线AB与 相切于点C，AO交 于点D，连接CD，OC.若 ，则 .
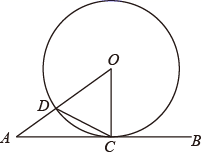16. 如图，在平面直角坐标系中，点A、B均在函数y＝ （k＞0，x＞0）的图象上，⊙A与x轴相切，⊙B与y轴相切．若点A的坐标为（3，2），且⊙A的半径是⊙B的半径的2倍，则点B的坐标为 ．
17. 如图，在直角坐称系中，半径为1的⊙A圆心A的坐标为（﹣1，0），点P为直线y＝﹣ x+2上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是.
18. 如图1，平行四边形ABCD中，AB⊥AC，AB＝6，AD＝10，点P在边AD上运动，以P为圆心，PA为半径的⊙P与对角线AC交于A，E两点．不难发现，随着AP的变化，⊙P与平行四边形ABCD的边的公共点的个数也在变化．如图2，当⊙P与边CD相切时，⊙P与平行四边形ABCD的边有三个公共点．若公共点的个数为4，则相对应的AP的取值范围为 ．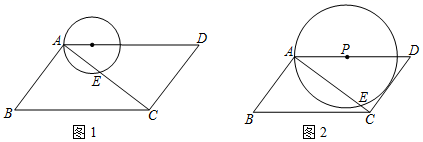
三、综合题
-
19. 如图，OA，OB为⊙O的半径，AC为⊙O的切线，连接AB．若∠B=25°，求∠BAC的度数．
20. 如图，AB是⊙O的直径，PB是⊙O的切线，连接AP交⊙O于点C。点D在⊙O上，∠CDB=45°，求证：AB=BP。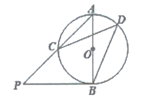
21. 如图，已知CD是△ABC中AB边上的高，以CD为直径的⊙O分别交CA，CB于点E，F，点G是AD的中点．求证：GE是⊙O的切线．
22. 如图，在 中， ，以 为直径作 ，过点 作 交 于 ， ．求证： 是 的切线．
23. 如图，以△ABC的边AB为直径画⊙O，交AC于点D，半径OEBD，连接BE，DE，BD，若BE交AC于点F，若∠DEB=∠DBC．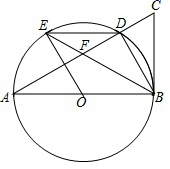
(1)、求证：BC是⊙O的切线；(2)、若BF=BC=2，求AB的长．24. 如图，△ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．
(1)、求证：∠ACD= ∠B；(2)、若BC＝6，AC＝8，求AD和CD的长．25. 如图1，正方形ABCD的边长为4，点P在边BC上，⊙O经过A，B，P三点.
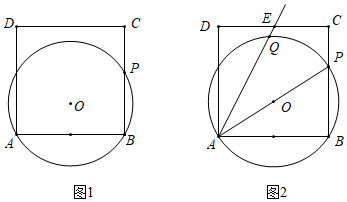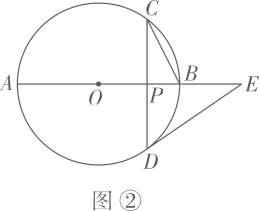
(1)、若BP＝3，判断边CD所在直线与⊙O的位置关系，并说明理由；(2)、如图2，E是CD的中点，⊙O交射线AE于点Q，当AP平分∠EAB时，求tan∠EAP的值.26. 已知AB为 的直径，EF切 于点D ， 过点B作 于点H交 于点C ， 连接BD ．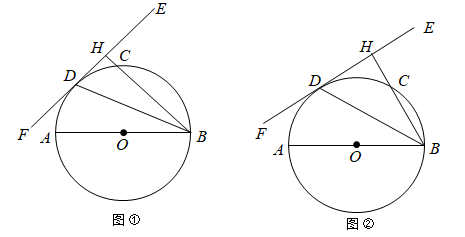
(1)、如图①，若 ，求 的大小；(2)、如图②，若C为弧BD的中点，求 的大小．
