2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.9 与圆有关的位置关系（1）
试卷更新日期：2022-01-18 类型：一轮复习
一、单选题
-
1. 半径为5的⊙O，圆心在直角坐标系的原点O，则点P（3，－4）与⊙O的位置关系是（ ）A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定2. 同一平面内， 一个点到圆的最小距离为 ， 最大距离为 ， 则该圆的半径为 （ ）A、 或 B、 或 C、 或 D、 或3. ⊙O的直径为10，圆心O到直线l的距离为4，则直线l与⊙O的位置关系是（ ）A、相交 B、相切 C、相离 D、无法确定4. 如图PA、PB分别与⊙O相切于A．B两点，点C为⊙O上一点，连接AC．BC，若∠ACB=60°，则 的度数为（ ）
A、60° B、65° C、 D、5. 如图，PA和PB是⊙O的切线，点A和B的切点，AC是⊙O的直径，已知∠P＝50°，则∠ACB的大小是（ ）
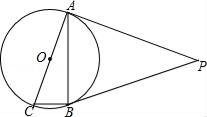A、65° B、60° C、55° D、50°6. 已知PA ， PB是⊙O的切线，A ， B是切点，点C是⊙O上不同于点A、点B的一个动点，若∠P＝54°，则∠ACB的度数是（ ）A、63° B、117° C、53°或127° D、117°或63°7. 已知矩形ABCD的边AB=15，BC=20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是（ ）.A、r＞15 B、15＜r＜20 C、15＜r＜25 D、20＜r＜258. 如图，点A的坐标为（﹣3，2），⊙A的半径为1，P为坐标轴上一动点，PQ切⊙A于点Q ， 在所有P点中，使得PQ长最小时，点P的坐标为（ ）
A、（0，2） B、（0，3） C、（﹣2，0） D、（﹣3，0）9. 如图，直线 与x轴、y 轴分别相交于点A、B两点，圆心P的坐标为（2，0）.⊙P与y轴相切于点O，若将⊙P沿x轴向左移动，当⊙P与该直线相交时，横坐标为整数的点P的个数是（ ）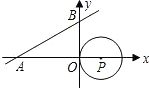
A、5 B、6 C、7 D、810. 如图， 的圆心 的坐标为 ，半径为1，直线 的表达式为 ， 是直线 上的动点， 是 上的动点，则 的最小值是（ ）
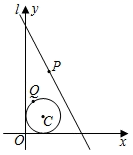A、 B、 C、 D、二、填空题
-
11. 点P(4，-3)与圆心在原点O，半径为5的⊙O的位置关系是12. 平面上一点P到⊙O上一点的距离最长为6cm，最短为2cm，则⊙O的半径为.13. 圆的直径是 ，如果圆心与直线的距离是 ，那么该直线和圆的位置关系是.14. 如图，已知圆O为Rt△ABC的内切圆，切点分别为D、E、F，且∠C=90°，AB=13，BC=12，则圆O的半径为。
15. 如图，PA，PB分别切⊙O于A，B，并与⊙O的切线，分别相交于C，D，已知△PCD的周长等于10cm，则PA=cm．
16. 如图，在Rt ACB中，∠ACB＝90°，AB＝4，∠BAC＝60°，D是边AC上的一个动点，连接BD，作CE⊥BD于点E，连接AE，则AE长的最小值为.
17. 在△ABC中，若O为BC边的中点，则必有：AB2＋AC2＝2AO2＋2BO2成立.依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE＝4，EF＝3，点P在以DE为直径的半圆上运动，则 的最小值为.
18. 如图，一次函数 与反比例函数 的图象交于点A，B，点P在以 为圆心，1为半径的⊙C上，Q是 的中点，若 长的最大值为 ，则k的值为.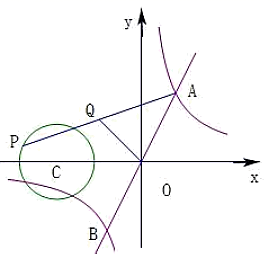
三、综合题
-
19. 如图， ， 分别与 相切于 两点，若 ，求 的度数．
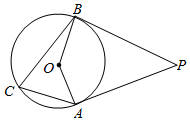20.（1）已知⊙O的直径为10cm，点A为⊙O外一定点，OA=12cm，点P为⊙O上一动点，求PA的最大值和最小值．
（2）如图：
=
， D、E分别是半径OA和OB的中点．求证：CD=CE．
21. 如图，公路 MN 和公路 PQ 在点 P 处交会，且∠QPN=30°．点 A 处有一所中学，AP=160m，一辆拖拉机从 P 沿公路 MN 前行，假设拖拉机行驶时周围 100m 以内会受到噪声影响，那么该所中学是否会受到噪声影响，请说明理由，若受影响，已知拖拉机的速度为 18km/h，那么学校受影响的时间为多长？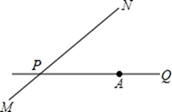
22. 如图，△ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．
(1)、求证：∠ACD= ∠B；(2)、若BC＝6，AC＝8，求AD和CD的长．23. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．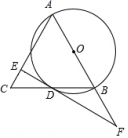
(1)、判断直线DE与⊙O的位置关系，并说明理由；(2)、如果AB=5，BC=6，求DE的长．24. 如图，已知 中， ，以 为直径的 交 于点 ， 为 中点， ，垂足为点 ，连接 ．
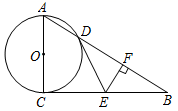(1)、求证： 是 的切线；(2)、若 ， ，求 的直径．25. 如图，矩形ABCD中，AB=8，BC=12，E是BC边的中点，点P在线段AD上，过P作PF⊥AE于F，设PA=x.
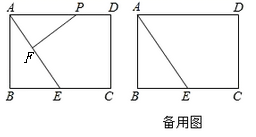(1)、求证：△PFA∽△ABE；(2)、当点P在线段AD上运动时，是否存在实数x，使得以点P，F，E为顶点的三角形也与△ABE相似？若存在，请求出x的值；若不存在，请说明理由；(3)、探究：当以D为圆心，DP为半径的⊙D与线段AE只有一个公共点时，请直接写出DP满足的条件：.26. 已知 的两边分别与⊙O相切于点A，B，⊙O的半径为r．
(1)、如图1，点C在点A，B之间的优弧上， ，则 ；(2)、如图2，点C在圆上运动，当 最大时（即连接 并延长交⊙O于点C），连接 ， ，①求证： ；
②若 交⊙O于另一点D， ，求图中对应的阴影部分的周长（用含r的式子表示）．
27. 已知平面直角坐标系中，点P（ ）和直线Ax＋By＋C＝0（其中A，B不全为0），则点P到直线Ax＋By＋C＝0的距离d可用公式 来计算.例如：求点P（1，2）到直线y＝2x＋1的距离，因为直线y＝2x＋1可化为2x－y＋1＝0，其中A＝2，B＝－1，C＝1，所以点P（1，2）到直线y＝2x＋1的距离为： .
根据以上材料，解答下列问题：
(1)、求点M（0，3）到直线 的距离；(2)、在（1）的条件下，⊙M的半径r ＝ 4，判断⊙M与直线 的位置关系，若相交，设其弦长为n，求n的值；若不相交，说明理由.28. 如图.在 中， ， ， ， 是 的中位线，连结 ，点 是边 上的一个动点，连结 交 于 ，交 于 .
(1)、当点 是 的中点时，求 的值及 的长(2)、当四边形 与四边形 的面积相等时，求 的长：(3)、如图2.以 为直径作 .①当 正好经过点 时，求证： 是 的切线：
②当 的值满足什么条件时， 与线段 有且只有一个交点.